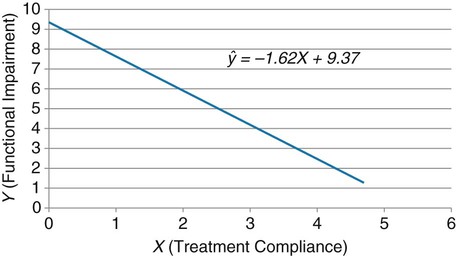
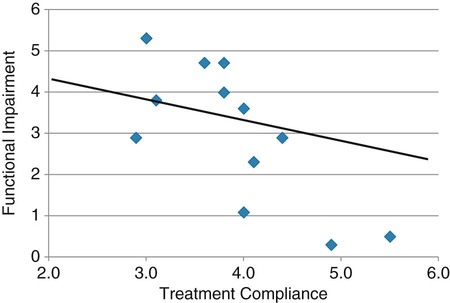
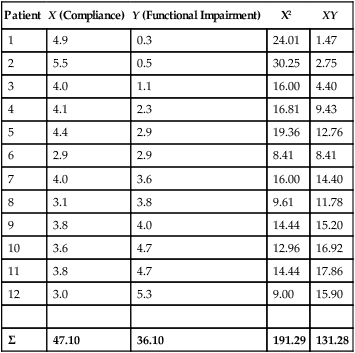
Simple linear regression provides a means to estimate the value of a dependent variable based on the value of an independent variable. Simple linear regression is an effort to explain the dynamics within the scatter plot by drawing a straight line (the line of best fit) through the plotted scores. This line is drawn to explain best the linear relationship or association between two variables. Knowing that linear relationship, we can, with some degree of accuracy, use regression analysis to predict the value of one variable if we know the value of the other variable (Cohen & Cohen, 1983). Figure 24-1 illustrates the linear relationship between treatment compliance (independent variable) and posttreatment functional impairment (dependent variable) among patients with chronic pain. As shown in the scatter plot, there is a strong inverse relationship between the two variables. Higher levels of treatment compliance are associated with lower levels of functional impairment. y = dependent variable (outcome) x = independent variable (predictor) b = slope of the line (beta, or what the increase in value is along the x-axis for every unit of increase in the y value) a = y-intercept (the point where the regression line intersects the y-axis) Table 24-1 displays how one would arrange data to perform linear regression by hand. Regression analysis is conducted by a computer for most studies, but this calculation is provided to increase your understanding of the aspects of regression analysis and how to interpret the results. This example uses actual clinical data obtained from adults with a painful injury who received multidisciplinary pain management. The calculation in this chapter includes a subset of the study data belonging to those patients (n = 12) with the highest levels of coping skills (Cipher, Fernandez, & Clifford, 2002). A subset was selected for this illustration so that the computation example would be small and manageable. In actuality, studies involving linear regression need to be adequately powered, so they employ a larger sample (Aberson, 2010; Cohen & Cohen, 1983). The strength of this example is that the data are actual, unmodified clinical data from a study. TABLE 24-1 Computation of Linear Regression Equation The first variable in Table 24-1 is the patient’s level of treatment compliance—the predictor or independent variable (x) in this analysis. The second variable is the patient’s posttreatment level of functional impairment—the dependent variable (y). Treatment compliance was assessed by patients’ scores on the Cognitive Psychophysiological Treatment Clinical Rating Scales (Clifford, Cipher, & Schumacker, 2003), which yields an overall compliance score with higher numbers representing better levels of compliance with the pain management treatment regimen. Functional impairment was represented by patients’ scores on the Interference subscale of the Multidimensional Pain Inventory (Kerns, Turk, & Rudy, 1985), with higher scores representing more functional impairment. The null hypothesis being tested is: Treatment compliance is not a significant predictor of posttreatment functional impairment among patients undergoing pain management. The data in Table 24-1 are arranged in columns, which correspond to the elements of the formula. The summed values in the last row of Table 24-1 are inserted into the appropriate places in the formula. From the values in Table 24-1, we know that n = 12, ΣX = 47.10, ΣY = 36.10, ΣX2 = 191.29, and ΣXY = 131.28. These values are inserted into the formula for b, as follows: From Step 1, we know that b = −1.62, and we plug this value into the formula for a: Step 3: Write the new regression equation: The predicted ŷ is 1.43. This procedure would be continued for the rest of the subjects, and the Pearson correlation between the actual functional impairment levels (y) and the predicted functional impairment levels (ŷ) would yield the multiple R value. In this example, R = 0.75. The higher R, the more likely that the new regression equation accurately predicts y because the higher the correlation, the closer the actual y values are to the predicted ŷ values. Figure 24-2 displays the regression line where the x-axis represents possible treatment compliance values, and the y-axis represents the predicted functional impairment levels (ŷ values). Step 5: Determine whether the predictor variable significantly predicts y. After establishing the statistical significance of the R value, it must be examined for clinical importance. This examination is accomplished by obtaining the coefficient of determination for regression—which simply involves squaring the R value. R2 represents the percentage of variance in y explained by the predictor. In our example, R was 0.75, and R2 was 0.56. Multiplying 0.56 × 100% indicates that 56% of the variance in posttreatment functional impairment can be explained by knowing the patients’ level of treatment compliance (Cohen & Cohen, 1983). R2 is most helpful in testing the contribution of the predictors in explaining an outcome when more than one predictor is included in the regression model. In contrast to R, R2 for one regression model can be compared with another regression model that contains additional predictors (Cohen & Cohen, 1983). For example, Cipher et al. (2002) added another predictor, the patients’ coping style, to the regression model of functional impairment. The R2 values of both models were compared, the first with treatment compliance as the sole predictor and the second with treatment compliance and copying style as predictors. The R2 values of the two models were statistically compared to indicate whether the proportion of variance in ŷ was significantly increased by including the second predictor of coping style in the model.
Using Statistics to Predict
![]() http://evolve.elsevier.com/Grove/practice/
http://evolve.elsevier.com/Grove/practice/
Simple Linear Regression
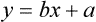
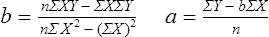
Calculation of Simple Linear Regression
Patient
X (Compliance)
Y (Functional Impairment)
X2
XY
1
4.9
0.3
24.01
1.47
2
5.5
0.5
30.25
2.75
3
4.0
1.1
16.00
4.40
4
4.1
2.3
16.81
9.43
5
4.4
2.9
19.36
12.76
6
2.9
2.9
8.41
8.41
7
4.0
3.6
16.00
14.40
8
3.1
3.8
9.61
11.78
9
3.8
4.0
14.44
15.20
10
3.6
4.7
12.96
16.92
11
3.8
4.7
14.44
17.86
12
3.0
5.3
9.00
15.90
Σ
47.10
36.10
191.29
131.28
Calculation Steps
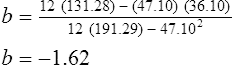
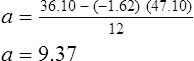
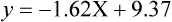
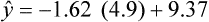
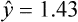
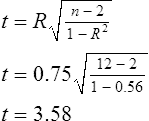
![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


Using Statistics to Predict
Get Clinical Tree app for offline access