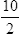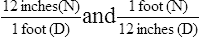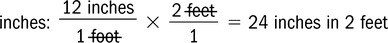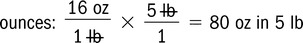• Examine a problem to identify the desired units for the answer. • Examine a problem to identify the quantity and units on hand that need to be converted. • Select and orient appropriate conversion factors. • Analyze the dimensional analysis (DA) setup to determine whether it will yield the desired answer units. • Solve basic arithmetic and simple metric medication equations using DA and units and number cancellation. There are several advantages to learning the DA method of solving equations: 1. It is a simple, organized system for setting up problems. 2. Problems can be set up in one step. 3. It allows the nurse to easily identify incorrect setup before calculations are carried out; a key factor in accuracy and efficiency. 4. It can be used for all medication problems, which cannot be said for all medication calculation methods. 5. An incorrect answer resulting from incorrect setup can be immediately identified. Conversion Factor An expression of equivalent amounts for two entities, such as 12 inches = 1 foot, 3 feet = 1 yard, 5280 feet = 1 mile, 1000 mg = 1 g, 250 mg/1 tablet, $20/1 hr, and 5 mg/10 mL. Dimensional Analysis A practical scientific method used to solve mathematical equations with an emphasis on units of measurement to set up the equation. The method requires three elements: desired answer units, given quantity and units to convert, and conversion factors. Dimension Unit of mass (or weight), volume, length, time, and so on, such as milligram (mass or weight), teaspoon (volume), liter (volume), meter (length), and minute (time). Equation Expression of an equal relationship between mathematical expressions on both sides of an equals sign, such as 2x = 4, 3 × 2 = 6, and Factors In DA, the data (numbers and units) that are entered in an equation in fraction form. In general, the word factor denotes anything that contributes to a result. The term has different meanings in different contexts. Label Descriptor of type, not necessarily a unit of dimension, such as 4 eggs, 4 dozen eggs, 1 tsp Benadryl, 100 mg tablets, 2 liters of 5% dextrose in water. Numerical Orientation of a Fraction Form Contents of the numerator (N) and denominator (D), such as Ratio Relationship between two different entities, such as 10 mg per tablet, 1 g per capsule, and 2 boys for each 2 girls. Unit *Descriptor of dimension, such as length, weight, and volume, for example, 2 inches ointment, 3 m height, 1 qt water, 250 mg antibiotic, 2 tbs Milk of Magnesia, and 6 kg body weight. In the first example, 2 is a quantity and inches is the unit of dimension. In the last example, 6 is a quantity and kilograms is the unit of dimension. *The word unit has different meanings in different contexts. Other definitions will be provided later in the text when relevant to the topic. RAPID PRACTICE 2-1 Essential Vocabulary Review Estimated completion time: 10 minutes Answers on page 488 Directions: Study the vocabulary to supply the requested information. 1. What are the three required elements of a DA-style equation? ___________ 2. What is the difference between a quantity and a unit? __________ 3. What is a conversion factor? _____________ 4. In the fraction ¾, what is the numerical orientation of 3? (Is it in the numerator or the denominator?) ___________________________ 5. In the fraction ⅛, what is the numerical orientation of 8? (Is it in the numerator or the denominator?) __________________________ 1. Write the desired answer on the left as a reminder. 2. Enter a factor in fraction form with a numerator that contains the desired answer units. (This will be called the starting factor in the equation.) 3. Enter the given factor that needs to be converted, positioning it to be cancelled. 4. When all unwanted units are cancelled and only the desired answer units remain, estimate the size of the answer, then multiply. How many inches are in 2 feet? Conversion factor: 12 inches = 1 foot. The final DA equation will be written like this: 1. What are the three main elements of a DA equation that must be identified before the setup? (Use brief phrases.) How many ounces (oz) are in 5 pounds (lb)? Conversion factor: 16 oz = 1 lb The final equation will be written like this:
Dimensional Analysis Calculations
Introduction
= 5. When an equation is solved, the values on both sides of the equals sign have equivalent value.
.
Setup of a Simple Equation Using Dimensional Analysis
Before multiplication, recheck the setup: After all unwanted units (feet) are canceled, only the desired answer units should remain. Estimate: the answer will be around 24 inches, larger than the given quantity of feet. These two checks help prevent setup and math errors.
Even if the setup is correct and even if both sides of the equation are equal, the answer may be wrong. Wrong data entry and incorrect multiplication will yield a wrong answer. DA is one of the best methods of preventing a setup error, and the final math equality on both sides of the equation is very easy to prove. However, DA cannot prevent operator numerical entry errors and careless handwriting that can be misread.
Dimensional Analysis Calculations
