Chapter 24
Diagnostic Reasoning in Physical Diagnosis1
Medicine is a science of uncertainty and an art of probability. One of the chief reasons for this uncertainty is the increasing variability in the manifestations of any one disease.
Sir William Osler (1849–1919)
Art, Science, and Observation
This is one of the most important chapters of the book, because it considers the methods and concepts of evaluating the signs and symptoms involved in diagnostic reasoning. The previous chapters discuss the “science” of medicine by explaining the techniques for interviewing and performing the physical examination. The ability to make the “best” decision in the presence of uncertainty is the “art” of medicine. But there are rules and standards for the practice of this art, and these are the focus of this chapter.
The primary steps in this process involve the following:
Data collection is the product of the history and the physical examination. These can be augmented with laboratory and other test results such as blood chemistry profiles, complete blood cell counts, bacterial cultures, electrocardiograms, and chest radiographs. The history, which is the most important element of the database, accounts for more than 70% of the problem list. The physical examination findings contribute an additional 20% to 25% of the database; less than 10% of the database is related to laboratory and other test results.
Data processing is the clustering of data obtained from the history, physical examination, and laboratory and imaging studies. It is rare for patients to have a solitary symptom or sign of a disease. They more commonly complain of multiple symptoms, and the examiner may find several related signs during the physical examination. It is the job of the astute observer to fit as many of these clues together into a meaningful pathophysiologic relationship. This is data processing.
For example, suppose the interviewer obtains a history of dyspnea, cough, earache, and hemoptysis. Dyspnea, cough, and hemoptysis can be grouped together as symptoms suggestive of cardiopulmonary disease. Earache does not fit with the other three symptoms and may be indicative of another problem. For another patient who complains of epigastric burning relieved by eating and whose stool is found to contain blood, this symptom and this sign should be studied together. These data suggest an abnormality of the gastrointestinal tract, possibly a duodenal ulcer. Although patients usually have multiple symptoms or signs from a pathologic condition, they may not always manifest all the symptoms or signs of the disease being considered. For instance, the presence of polyuria and polydipsia in a patient with a family history of diabetes is adequate to raise the suspicion that a lateral rectus palsy may be related to diabetes, even if diabetes has not previously been diagnosed in this patient. In another patient, a 30-pound weight loss, anorexia, jaundice, and a left supraclavicular lymph node are suggestive of gastric carcinoma with liver metastasis to the porta hepatis. This illustrates the concept of data processing multiple symptoms into a single diagnosis. The process has sometimes been likened to the rule of Occam’s razor: The simplest theory is preferable—in this case, that all the symptoms can be explained by one diagnosis. Although it is a useful rule to keep in mind, it is not always applicable.
Problem list development results in a summary of the physical, mental, social, and personal conditions affecting the patient’s health. The problem list may contain an actual diagnosis or only a symptom or sign that cannot be clustered with other bits of data. The date on which each problem developed is noted. This list reflects the clinician’s level of understanding of the patient’s problems, which should be listed in order of importance. Table 24-1 is an example of a problem list.
Table 24–1
Example of a Problem List
| Problem | Date | Resolved |
| 1. Chest pain | 6/28/12 | |
| 2. Acute inferior myocardial infarction | 1/30/10 | 2/15/10 |
| 3. Colon cancer | 4/30/08 | 6/3/08 |
| 4. Diabetes mellitus | 2003 | |
| 5. Hypertension | 1997 | |
| 6. “Red urine” | 6/10/09 | 7/1/09 |
| 7. Distress over son’s drug abuse | 1/12 |
The presence of a symptom or sign related to a specific problem is a pertinent positive finding. For example, a history of gout and increased uric acid level are pertinent positive findings in a man suffering from excruciating back pain radiating to his testicle. This patient may be suffering from renal colic secondary to a uric acid kidney stone. The absence of a symptom or sign that, if present, would be suggestive of a diagnosis is a pertinent negative finding. A pertinent negative finding may be just as important as a pertinent positive finding; the fact that a key finding is not present may help rule out a certain diagnosis. For example, the absence of tachycardia in a woman with weight loss and a tremor makes the existence of hyperthyroidism less likely; the presence of tachycardia would strengthen the likelihood of hyperthyroidism.
An important consideration in any database is the patient’s demographic information: sex, age, ethnicity, and area of residence. A man with a bleeding disorder dating from birth is likely to have hemophilia. A 65-year-old person with exertional chest pain is probably suffering, statistically, from coronary artery disease. A 26-year-old African-American patient with multiple episodes of severe bone pain may be suffering from sickle cell anemia. A person living in the San Joaquin Valley who has pulmonary symptoms may have coccidioidomycosis. This information is often suggestive of a unifying diagnosis, but the absence of a “usual” finding should never totally exclude a diagnosis.
It has been said, “Common diseases are common.” This apparently simplistic statement has great merit because it underlines the fact that the observer should not assume an exotic diagnosis if a common one accurately explains the clinical state. (In contrast, if a common diagnosis cannot account for all the symptoms, the observer should look for another, less common diagnosis.) It is also true that “Uncommon signs of common diseases are more common than common signs of uncommon diseases.”
Finally, “A rare disease is not rare for the patient who has the disease.” If a patient’s symptoms and signs are suggestive of an uncommon condition, that patient may be the 1 in 10,000 with the disease. Nevertheless, statistics based on population groups provide a useful guide in approaching clinical decision-making for individual patients.
Diagnostic Reasoning from Signs and Symptoms
Unfortunately, decisions in medicine can rarely be made with 100% certainty. Probability weights the decision. Only if the cluster of symptoms, signs, and test results is unequivocal can the clinician be certain of a diagnosis. This does not occur often. How, then, can the clinician make the “best” decision—best in light of current knowledge and research?
Laboratory tests immediately come to mind. But signs and symptoms obtained from the patient’s history and physical examination perform the same function as laboratory tests, and the information and results obtained from signs, symptoms, and tests are evaluated in the same way and are subject to the same rules and standards of evidence for diagnostic reasoning. Also, signs and symptoms actually account for more (90%) of the developing problem list than do laboratory test results (<10%).
Sensitivity and Specificity
Throughout this text, signs and symptoms have been described according to their operating characteristics: sensitivity and specificity. These operating characteristics, which also apply to laboratory tests, indicate the usefulness of the sign, symptom, or test to the clinician in making a diagnosis. Sensitivity is equal to the true-positive rate, or the proportion of positive test results in individuals with a disease. Sensitivity, therefore, is based solely on patients with the disease. Specificity is equal to the true-negative (TN) rate, or the proportion of negative test results in individuals without a disease. Specificity, therefore, is based only on individuals without the disease. A false-positive (FP) finding refers to a positive test result in an individual without the disease or condition. Thus a sign, symptom, or test with 90% specificity can correctly identify 90 of 100 normal individuals; findings in the other 10 individuals are FP, and the FP rate is 10%. If a test result or observation is negative in a person with the disease, the result is termed false negative (FN).
The 2 × 2 table is useful for representing the relationship of a test, symptom, or sign to a disease. D+ indicates the presence of the disease; D− indicates the absence of the disease; T+ is a positive test result, or the presence of a symptom or sign; T− is the absence of a positive test result, or the absence of a symptom or sign. Each of the cells of the table represents a set of patients. Consider the following 2 × 2 table:
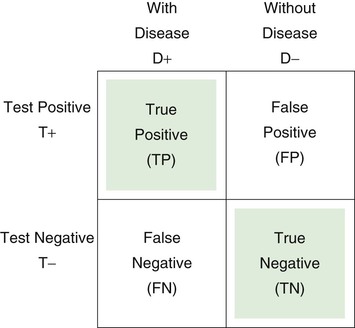
Sensitivity is defined as the number of true positive (TP) results divided by the number with disease (i.e., the total of the TP and the FN results):
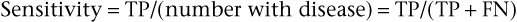
Specificity is defined as the number of TN results divided by the number without disease (i.e., the total of FP results and TNs):
Substituting numbers:
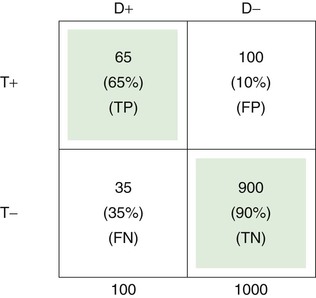
The upper left cell of the 2 × 2 table indicates that 65 of 100 patients with a certain disease (65%) had a certain positive test result or symptom or sign. Thus the test has a TP rate of .65, or a sensitivity of 65%.
The TN rate is .90, as indicated in the lower right cell; this means that 900 of 1000 individuals without the disease (90%) did not have a positive test result or symptom or sign. Therefore the specificity of the test is 90%.
The FP rate is .10, meaning that 100 of 1000 in the normal population (10%) had the finding for some reason, without having the disease in question. This is shown in the upper right cell.
Finally, the lower left cell indicates that the test result, symptom, or sign is absent in 35 of 100 patients with the disease. Thus the FN rate is 35%.
Note that the TP rate plus the FN rate equals 1; the FP rate plus the TN rate also equals 1. If the disease is aortic stenosis and the symptom is syncope, then according to the preceding table, 65% of patients with aortic stenosis have syncope, and 35% do not; 90% of individuals without aortic stenosis do not have syncope, and 10% do.
Likelihood Ratio
Because sensitivity and specificity are used to measure different properties, a symptom, sign, or test has both sensitivity and specificity values: high sensitivity and high specificity, low sensitivity and low specificity, high sensitivity and low specificity, or low sensitivity and high specificity. Sensitivity and specificity are often combined to form the likelihood ratio (LR), which provides a unitary measure of the operating characteristics of a sign, symptom, or test. The LR is defined as the ratio of the TP rate to the FP rate:
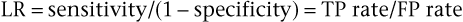
Thus the LR indicates the proportion of accurate to inaccurate positive test results. In the preceding example of syncope and aortic stenosis, where sensitivity = TP rate = .65, and 1 − specificity = FP rate = .10, the LR would be equal to .65/.10, or 6.5. In other words, a positive sign, symptom, or test result is 6.5 times more likely in patients with disease than in individuals without disease. In the example, the occurrence of syncope would be 6.5 times greater in patients with aortic stenosis than in individuals without it. Tests or signs with LRs greater than 10 are generally highly useful because they provide considerable confidence in diagnostic reasoning.
Ruling In and Ruling Out Disease
Sensitivity and specificity (and the LR) refer to properties of the symptom, sign, or test result that are invariant across different populations. This is true even though particular populations may differ with regard to the prevalence of the disease or condition in question. Sensitivity is based solely on patients with disease, and specificity is based solely on individuals without disease. Thus the relative sizes of the two groups—with disease and without disease—in the population of concern, which is the basis for the computation of prevalence, play no role in the computation of sensitivity and specificity. Sensitivity and specificity are simply the operating characteristics of the test and as such provide general information about the usefulness of the test for diagnostic reasoning with any population of patients. But in actual clinical practice, the clinician is concerned with the individual patient and whether that patient’s test results are predictive of disease. How certain can the clinician be that a patient has a disease if the test result is positive or if a symptom or sign is present? How certain can a clinician be that a person is healthy if a test result is negative or if a symptom or sign is absent? Typically, these questions are answered by computing the positive and negative predictive values, which are based on sensitivity and specificity but also take into account the prevalence of disease in the population of which the patient is a member.
First, however, consider two special cases of diagnostic reasoning in which clinical decisions can be based on only a knowledge of sensitivity and specificity. If the sensitivity of a given symptom, sign, or test is quite high, 90% or greater, and the patient has a negative result, the clinician can somewhat confidently rule out disease because so few patients with disease have a negative test result (<10%). Sackett (1992) devised the following acronym for this special case: Sensitive signs when Negative help rule out the disease (SnNout). In the absence of a highly sensitive sign, a person is most likely not to have the disease. The second special case occurs if the specificity of a given test, symptom, or sign is quite high, 90% or greater, and the patient has a positive result. The clinician can then somewhat confidently rule in disease because so few individuals without disease have a positive test result (<10%). Sackett’s acronym for this case is Specific signs when Positive help rule in the disease (SpPin). In the presence of a highly specific sign, a person is most likely to have the disease.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


