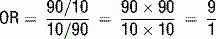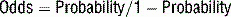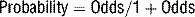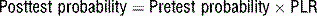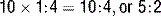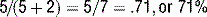1 What does the sensitivity of a diagnostic test measure?

Sensitivity is a measure of how effectively a diagnostic test can detect the disease in a patient who truly has the disease (true positive). In other words, sensitivity measures the proportion of individuals with a disease who test positive for it.

Sensitivity can be calculated by dividing the number of true positives by the total number of people tested with the disease: true positives/(true positives + false negatives), or a/(a + c) in the 2 × 2 table (Table 25-1). You can also calculate sensitivity by subtracting the false negative rate from 1 (i.e., sensitivity = 1 – false negative rate); however, you will seldom be given the false negative rate on boards.

Table 25-1 Sample 2 × 2 table

2 What does the specificity of a diagnostic test measure?

The specificity of a diagnostic test is a measure of how effectively the test can detect the absence of disease in a patient without the disease (true negative). It is an indication of how “specific” a positive test result is to the disease it is designed to detect. The greater the number of different conditions that cause a positive test result other than the disease the test is designed to detect, the less specific the test.

Specificity can be calculated by dividing the number of true negatives by the total number of people tested who do not have the disease: true negatives/(true negatives + false positives), or d/(b + d) in the 2 × 2 table). Specificity is also equal to 1 − false positive rate.

3 Quick terminology review: Cover the right column in Table 25-2 and define each of the terms in the left column

Table 25-2 Basic Terminology

4 How does the sensitivity of a test relate to its specificity?

Sensitivity and specificity move in opposite directions as test parameters change. In other words, as sensitivity increases, specificity decreases, and vice versa. This occurs because, in order to improve the sensitivity of a test (i.e., detect more people with a disease of interest), the limits on what results are considered to be positive must be made less stringent. In detecting more people with the disease, the test will therefore also yield positive results in more people without the disease.

For example, the rheumatoid factor (RF) is often used to aid in the diagnosis of rheumatoid arthritis (RA). RF is positive in 70% of patients with RA. If you want to catch more cases of patients with RA, you can use the erythrocyte sedimentation rate (ESR). The ESR is positive in 90% of patients with RA. However, with this increased sensitivity comes decreased specificity. ESR is very nonspecific and can be positive in any inflammatory process, from pneumonia to temporal arteritis. Given its high sensitivity, a negative ESR is helpful in ruling out inflammatory disease (see later discussion).

SPIN and SNOUT are useful mnemonics. SPIN tells us that specific tests rule in disease. That is, the more specific a test, the more likely it is that a positive result indicates real disease. SNOUT tells us that sensitive tests rule out disease. That is, the more sensitive a test, the more likely that a negative result rules out disease. In serious diseases that can be treated effectively if detected, a greater sensitivity is desired (often at the expense of specificity).

5 What information is given by the relative risk?

The relative risk (RR) is a ratio that compares event rates in one group versus another. It can be calculated by dividing the probability of occurrence of disease (incidence) in the exposed group by the probability of occurrence of disease in the unexposed group.

For example, in the 2 × 2 table (Table 25-3), the probability of lung cancer in smokers is 90/100 or .90. The probability of lung cancer in nonsmokers is 10/100, or .10. Therefore, the RR for smoking is .90/.10, or 9. An RR of 9 implies that smokers are 9 times more likely to get lung cancer than nonsmokers.

Table 25-3 Smoking Exposure and Lung Cancer

An RR of >1 means that the event is more likely to occur in the exposed group. An RR of <1 means the event is less likely to occur in the unexposed group. An RR of 1 means that there is no difference between the groups.

6 What information is given by the odds ratio?

The odds ratio (OR) also compares event rates between two groups but is calculated by comparing odds rather than probabilities.

For the preceding example, the OR can be calculated by dividing the odds of smokers’ developing lung cancer (90:10) by the odds of nonsmokers’ developing lung cancer (10:90), as follows:

As with RR, an OR of 1 means the event was equally likely in both groups, an OR of >1 means the event was more likely to occur in the exposed group, and an OR of <1 means the event was more likely to occur in the unexposed group.

You must know that RR and ORs are used for different types of tests. RR is used for cohort studies and randomized controlled trials (study types that measure risk of outcome based on exposure status) because those studies allow for calculation of the percentages of participants that are affected. ORs are usually used in case-control studies, which approximate odds of exposure based on rates of outcome occurrence in which percentages cannot be calculated. You will read more about types of tests later in this chapter.

The RR and ORs for one study may be drastically different (as in the preceding example) for common events but approximate each other for rare events.

7 What is the difference between probability and odds and how are they measured?

Probability is measured along a continuum from 0 to 1, where 0 means the event is certain not to happen and 1 means the event is certain to happen.

Odds are measured along a continuum from 0 to infinity.

Probabilities can be easily converted to odds, and vice versa.

and

If the pretest probability of a certain diagnosis is 90%, then the odds are .9/1 − .9 = 9 (sometimes stated as “9 to 1”).

8 What is the positive predictive value? negative predictive value?

The positive predictive value (PPV) is the probability that, given a positive test result, the disease in question is actually present. The negative predictive value (NPV) is the probability that disease is absent if there is a negative test result. If a 2 × 2 table is provided, the PPV can be calculated by dividing the number of true positives by the total number of positive test results (a/a + b) and the NPV can be calculated by dividing the number of true negatives by the total number of negative test results (d/c + d) (Table 25-4).

Table 25-4 Calculating Predictive Values Using the 2 × 2 Table

Because a 2 × 2 table is not normally provided, the PPV can also be calculated if the sensitivity and specificity of the test and the prevalence of the disease being tested are known, as discussed later.

What happens to the positive and negative predictive values as disease incidence changes? This is the type of question you might see on boards— is the reason why setting up the 2 × 2 table can be so helpful. If disease incidence increases, the numbers in the left column (true positives [TP] and false negatives [FN]) will both increase. Because PPV = TP/(TP + FP), PPV will increase if the number of TP increase. NPV, on the other hand, will decrease as incidence increases because FN increase in value. Recall that NPV = TN/(TN + FN), where TN = true negatives.

9 What is the positive likelihood ratio?

The positive likelihood ratio (PLR) reflects how much a positive test result increases the probability of disease being present. The higher the ratio, the more likely it is that disease is present. This ratio is calculated as the sensitivity divided by 1 − specificity. For example, if the sensitivity is 85% and the specificity is 90%, the PLR is 0.85/(1 − 0.9) = 8.5. Consequently, the more sensitive and specific the test is, the higher the PLR. The PLR is now widely used in evidence-based medicine because of the ease with which it can be used to calculate the PPV of a test.

10 How is the positive likelihood ratio used to calculate the positive predictive value?

This is done by converting the prevalence of a disease to an odds ratio (e.g., 20% to 1:4) and then multiplying the first part of the ratio by the PLR (8.5 × 1:4 = 8.5:4). Then the ratio is converted back to a percentage: 8.5/(8.5 + 4) = 0.68 or 68%.

Let’s assume the pretest probability of coronary artery disease in a 40-year-old man with diabetes who smokes is 20% and that the presence of a “positive” exercise stress test has a PLR of 10.

Expressed in odds, 20% is 1:4, so the PPV of the exercise stress test is calculated as follows:

So the probability that this man has coronary artery disease if he has a positive stress test is 71%, which is substantially up from his pretest probability of 20%.

11 What is meant by the reliability of a test?

Reliability (precision) is the consistency or repeatability of a test. A test is reliable if it produces the same results each time when the conditions are the same. For example, the SAT exam would be considered reliable if a student could take it more than once and get close to the same score each time. It would not be considered a reliable test if the same student received dramatically different scores on two different days. Precision is improved by reduction in random error. Random error is unpredictable and affects all measurements. It is used to describe any deviations from the true value of a measurement that result from fluctuations in the readings provided by the measurement tool.

12 What is meant by the validity of a test?

Validity (accuracy) is a measure of how well a test result corresponds to what it claims to measure. In other words, a test result is considered valid if it closely matches the actual value of whatever is being measured. Note that this actual value is usually estimated using the gold standard test method. Validity is generally reduced through systematic error. For example, an IQ test that depends in part on reading comprehension is invalid because IQ should not depend on literacy. This is a systematic error in designing or conducting the test. Systematic error refers to deviations from the true value of a measurement that result from poor instrument calibration or flawed observation methods.

13 In statistical analyses of differences between groups, a P value is often included to reflect how significant the difference is. What is the meaning of this P value?

At its most basic level, the P value reflects the probability that the difference observed between groups could occur by chance alone. For example, if the P value is 0.05, there is a 5% chance that the difference observed could have been entirely due to random chance, and not due to whatever intervention was used in the experiment. Nevertheless, most of modern science considers a difference “significant” if there is a <5% (P < .05) chance that the difference could have occurred by random chance. Obviously, the smaller the P value, the smaller the probability that any difference was due to chance, and with that, the more convincing it is that the intervention evaluated was responsible for the difference.

14 What are the differences between type I and type II error? How is power related to type II error?

Type I (α) error refers to “false positive error.” In other words, α = the probability of claiming that a true difference exists between two means when in reality none exists. The “null hypothesis” (H₀) claims that there is no difference between two means. If a researcher claims a statistical difference between two groups when none exists and falsely rejects the null hypothesis, the researcher has committed a type I error.

By contrast, type II (β) error is “false negative error.” It refers to the probability of stating that no difference exists between the means of two values when in fact there truly is a difference. Type II error is an acceptance of the null hypothesis when it should indeed be rejected.

Let’s, for instance, say that we wish to determine the factors that influence the difference in the mean USMLE scores observed between two groups of medical students. We hypothesize that time spent studying for the USMLE could be significantly different between the two groups and may thus exhibit a causal relationship with the scores obtained by the students. We devise a method to measure this variable and do not find that this significantly differs between the two groups. If a difference truly exists, we have made a type II error in this case.

The term “statistical power” is a reflection of a study’s ability to correctly detect a difference between means when one truly exists. Power is equal to 1 − β. This makes good sense, right? Since β is the probability of committing a type II error (not detecting a difference that truly exists), power should inversely correlate with this value.

15 What are some determinants that can be used to evaluate the existence of a causal relationship between two variables?

16 What is the difference between prevalence and incidence?

Prevalence is the percentage of the population that currently has the disease. For example, 25% of Americans are obese, so the prevalence of obesity is 25%. Incidence refers to how many people develop a disease within a given time frame (usually annually). Thus, if 300,000 people are newly diagnosed with diabetes each year, the annual incidence of diabetes is 300,000.

17 How do the incidence and duration of a disease affect its prevalence?

The higher the incidence and the longer the duration of the disease, the greater the prevalence. Chronic diseases (e.g., arthritis) are unlikely to rapidly result in death, so their prevalence is high. Diseases that have a short duration (e.g., meningitis), either because they rapidly result in rapid death or because they resolve quickly, will have a low prevalence in the population. Incidence and prevalence are roughly equal in diseases that have a short duration.