Boundary Setting in Experimental-Type Designs
Key terms
Cluster sampling
Convenience sampling
Effect size
External validity
Nonprobability sampling
Population
Probability sampling
Purposive sampling
Quota sampling
Sample
Sampling
Sampling error
Sampling frame
Simple random sampling
Snowball sampling
Statistical power
Stratified random sampling
Systematic sampling
Target population
As discussed in Chapter 11, setting boundaries in experimental-type designs is one of the first action processes that occurs. Think about what you have learned thus far about experimental-type designs. What do you think are the characteristics of the process of setting boundaries in this research tradition? If you said the process is primarily deductive, prescribed, and determined before entering the field, you are correct.
Now, think about what would be the primary concern in setting boundaries in experimental-type research. The primary aim of boundary setting is to select a group of study participants, subjects, or objects who adequately represent the population that is the target of the study. This is a critical point on which all boundary-setting procedures are based in this research tradition. Now we examine how researchers who use the range of experimental-type designs actually approach the action process of selecting people, groups, or other entities for study participation.
In experimental-type design, the boundary-setting action process is basically deductive. This means that first, the researcher begins with a clear idea of what or whom he or she wants to study. The study group of interest to the investigator is called a population, defined as a group of persons, elements, or both that share a set of common characteristics as predefined by the investigator. The researcher must clearly define the characteristics of the population, which includes the individuals or units to be studied. Second, the researcher chooses a set of procedures by which to select a subset or sample from the population who will participate in the study. The individuals or units from the population who actually participate in the study are called a sample, which is a subset of the population. The process of selecting a subgroup or sample is called sampling.
Sampling process
The main purpose of sampling is to select a subgroup that can accurately represent the population. The intent is to be able to draw accurate conclusions about the population by studying a smaller group of elements (sample). The problem for the experimental-type researcher is how best to select a sample that is representative of an entire population. Accurate representation is critical to allow findings from the study sample to be generalized (applied) to the larger group (population) from which the sample is drawn.1,2
Sampling designs or procedures have been developed to increase the chances of selecting individuals or elements that will be most representative of the larger population from which they are drawn. The more representative the sample, the more assured the researcher will be that the findings from the sample also apply to the population. The extent to which findings from a sample apply to the population is called external validity, as discussed in Chapter 11. Most researchers conducting experimental-type designs attempt to maximize external validity by using one of the sampling procedures discussed in this chapter.
Investigators follow many action processes to draw a sample from a population. In this chapter, we discuss five basic steps common to the various experimental-type sampling processes (Box 13-1).
The first step in sampling involves the careful definition of a population. As defined earlier, a population is the complete set of elements that share a common set of characteristics and do not possess any characteristics identified by the researcher as “not to be included.” Examples of elements are persons, households, communities, hospitals, outpatient settings, and research studies on a common topic. The “element” is the unit of analysis included in the population, regardless of its type. Or, in the example of research studies, an investigator conducting a meta-analysis would specify the essential elements for each study that would be included, as well as characteristics of studies that would be excluded.
In a study of the management practices of hospitals, the investigator would be interested in the hospital as a whole, rather than the people in it. In this case, the hospital is the unit of analysis, and the sample is the specified number of hospitals participating in the study. However, in a study of the characteristics of older persons admitted to hospitals in the summer months, each patient, not the hospital as a whole, is the unit of analysis, and the sample is composed of the set of individuals selected for the study.
New investigators often ask how populations are identified and delimited. In experimental-type design, two issues are important to consider: (1) the purpose of the study and (2) the literature support for selecting or excluding population parameters. Thus, it is the investigator who uses previous work and a purposive lens to define or choose the characteristics or parameters of the population that are important to study. Consider the following two examples.
You are interested in studying the needs of parents caring for children with chronic illness. The first step in selecting your study sample would be to identify the specific characteristics of the larger population you are interested in examining. To identify population characteristics, you will need to identify the purpose of your inquiry and then consult the literature to see how other investigators have conceptualized the important population characteristics that need to be included and excluded.
You are conducting a needs assessment study as the basis for implementing a hospital-based transition intervention to assist parents of children with cystic fibrosis in their parenting. Because of the hospital policy regarding the age range of children in their cystic fibrosis unit, you decide to include parents caring for children between ages 3 and 8 years who have been diagnosed. On the basis of the literature, you may also decide to exclude cases in which both parents do not reside together, both are unemployed, or more than one other sibling is in the home. By establishing these inclusion and exclusion criteria, you will have defined a target population from the universe of parents caring for a child with a chronic illness.
By some definitions, the target population is an “ideal” only because the investigator cannot access such a population. However, in this chapter we define the target population as a useful entity, referring to the group of individuals or elements from which the investigator is able to select a sample. Each element of the target population may possess characteristics other than those specified by the investigator. However, each element must fit three criteria (Box 13-2).
How do investigators using experimental-type designs identify a population? First, the research question guides the investigator. Remember that all experimental-type questions include the population in which the variables and their relationships are being studied. Thus, the research question contains the basic lexical identification of the population. Second, the researcher uses the literature to clarify and provide support for establishing population parameters.
If an investigator is interested in studying persons with chronic mental illness, a vast body of literature provides clear descriptions and definitions of this broad category of individuals. An astute investigator may choose a well-accepted source, such as the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV),3 for a definition of chronic mental illness to structure parameters based on this knowledge.
The literature also helps to identify those characteristics that the investigator may want to exclude from the targeted population.
To isolate and not confound the major population parameter of interest, “chronic mental illness,” individuals may be excluded from the target population if they possess a primary physical diagnosis along with a psychiatric diagnosis, or if the mental illness is a secondary consequence of a traumatic head injury.
Consider another example.
You are interested in understanding the daily routines of persons with quadriplegia. What would be the steps you would follow? First, you would need to define the specific population characteristics of the group you want to study. Some guiding questions you would ask are listed in Box 13-3.
Reading how other researchers bound their studies is helpful in answering these questions. Your answers will lead to the development of specific criteria by which to include and exclude individuals. Additionally, as indicated earlier, to answer these questions, you will need to consider your purpose in conducting the study. Finally, you will need to refer to the practice and research literature for definitions of terms such as “quadriplegia” and “functional level.”
Defining a population is a critical step in sampling and must be done carefully and thoughtfully. How an investigator identifies a population shapes the nature and findings of a study.
Suppose you are interested in examining the health literacy of veterans who are wounded in Iraq. In your study, you define your population broadly as all soldiers who return home to Veterans Administration hospitals for treatment of physical injuries sustained in battle. You are surprised when you find an extremely low literacy level. In a similar study, your colleagues study the same population of wounded veterans but exclude those who have visual impairments and who speak English as a second language. The level of health literacy revealed in this study is very high, and thus the finding appears to contradict those from your study.
Including or excluding different population characteristics can change the outcomes of a study. In the example, including English-language competency and excluding potential confounding parameters, such as the inability to see print material, had a major impact on study findings. You must clearly articulate the criteria used for bounding your study. Also, when comparing findings from studies on a similar topic and target population, whether used in literature review or formal meta-analysis, you must carefully evaluate the differences in boundary setting among studies.
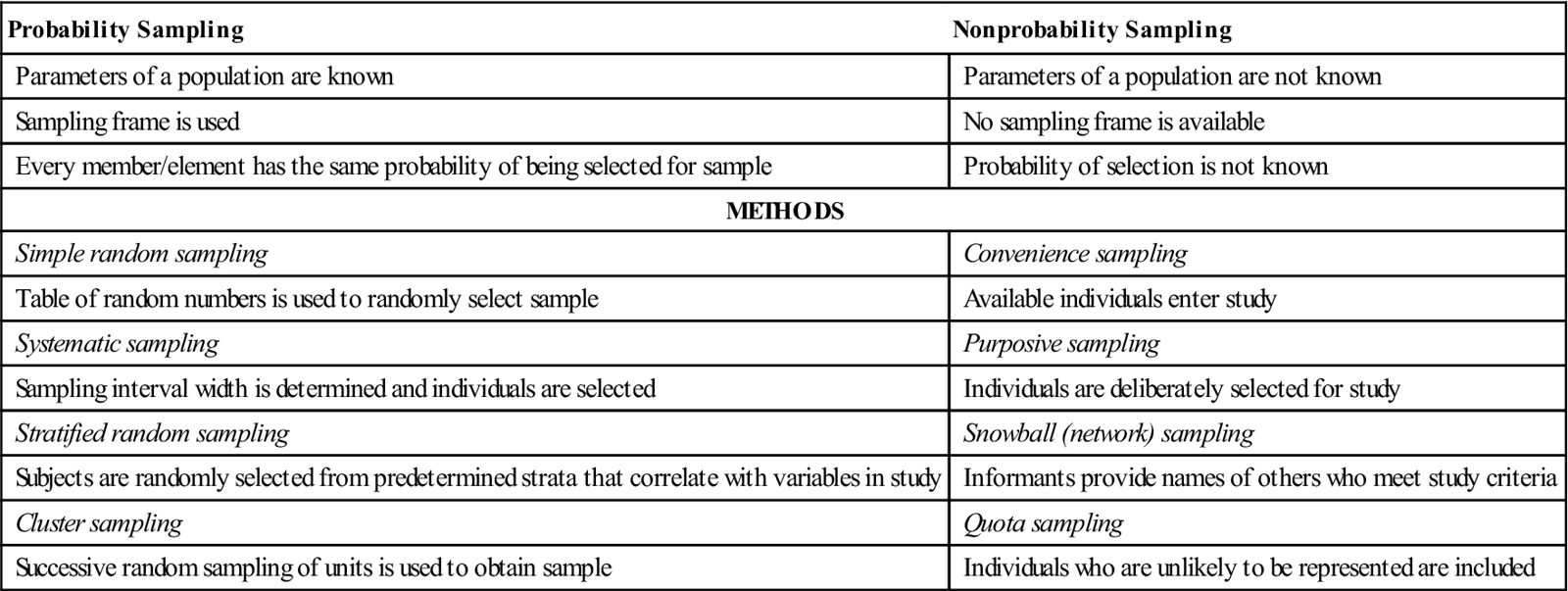
The second major step in boundary setting in experimental-type design involves drawing a sample from your specified population through the use of a sampling plan. There are two basic categories of sampling plans, probability sampling and nonprobability sampling. Table 13-1 provides an overview of the commonly used sampling plans discussed in this chapter.
TABLE 13-1
Summary of Common Sampling Plans Used in Experimental-Type Research
| Probability Sampling | Nonprobability Sampling |
| Parameters of a population are known | Parameters of a population are not known |
| Sampling frame is used | No sampling frame is available |
| Every member/element has the same probability of being selected for sample | Probability of selection is not known |
| METHODS | |
| Simple random sampling | Convenience sampling |
| Table of random numbers is used to randomly select sample | Available individuals enter study |
| Systematic sampling | Purposive sampling |
| Sampling interval width is determined and individuals are selected | Individuals are deliberately selected for study |
| Stratified random sampling | Snowball (network) sampling |
| Subjects are randomly selected from predetermined strata that correlate with variables in study | Informants provide names of others who meet study criteria |
| Cluster sampling | Quota sampling |
| Successive random sampling of units is used to obtain sample | Individuals who are unlikely to be represented are included |
Probability sampling
Probability sampling refers to those plans that are based on probability theory. The two basic principles of probability theory as applied to sampling are as follows: (1) the parameters of the population are known and (2) every member or element has an equal probability or chance of being selected for the sample. A third rationale, related to probability reasoning but not specific to guiding action, is the theoretical assumption that equal probably of being selected is accompanied by equal probability of being exposed to all influences that could otherwise provide potential confounding factors in your study.
The important point is that the probability of each element included in the study is known and greater than zero. By knowing the population parameters and the degree of chance that each element may be selected, an investigator can calculate the sampling error. Sampling error refers to the difference between the values obtained from the sample and the values that actually exist in the population. It reflects the degree to which the sample is actually representative of the population. The larger the sampling error, the less representative the sample is of the population and the more limited is the external validity of the study. The purpose of probability sampling is to reduce sampling error and to increase the external validity of a study.
To determine sampling error, we can derive a calculation called the “standard error of the mean,” which reflects the standard deviation of the sampling distribution and is designated SEm (see Chapter 19). Many statistical analytical tools used in experimental-type research are based on an assumption of probability: the assumption that a variable will be distributed in a population along a bell-shaped curve. The bell-shaped curve is a graphic depiction of what is expected to occur in a typical group. In other words, it is most probable that the majority of observations will be similar and will cluster around the average. More extreme observations, or those that are farther from the mean, are expected to be less frequent. The distance of a single score from the mean score is called “deviation.”
Assume you want to draw a sample of 50 older adults with cancer from a larger population of older patients with cancer, then evaluate them using a “life satisfaction” measure. Then you want to draw another sample of 50 older adults, then a third sample, and so forth. If you compute the mean score on life satisfaction for each sample, you will have what is called a “sampling distribution of means.”
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
