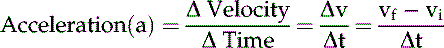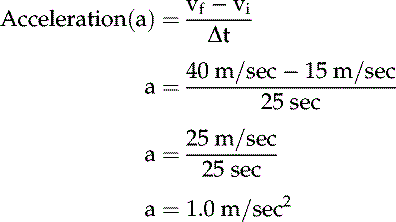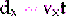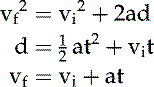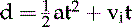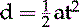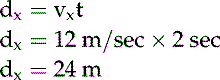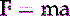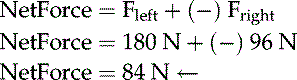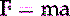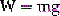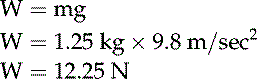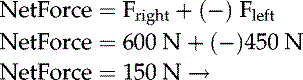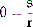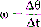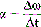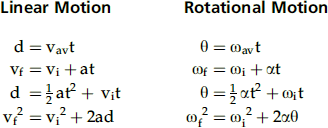Physics

8 Physics



Chapter outline


Nature of Motion

Acceleration

Projectile Motion

Newton’s Laws of Motion

Friction

Rotation

Uniform Circular Motion

Kinetic Energy and Potential Energy

Linear Momentum and Impulse

Universal Gravitation

Waves and Sound

Light

Optics

Atomic Structure

The Nature of Electricity

Magnetism and Electricity


Key terms


Acceleration


Average Speed


Binding Energy


Centripetal Acceleration


Force


Friction


Impulse Equation


Joules


Kinetic Energy


Law of Universal Gravitation


Momentum


Newton


Potential Energy


Projectile Motion


Reflection


Refraction


Scalar Quantity


Valence Electrons


Vector Quantity


Velocity


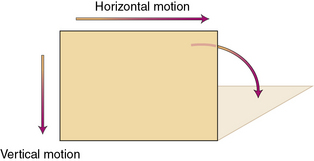
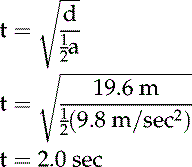
Members of the health professions, particularly medical imaging professionals, use the fundamental principles of physics on a daily basis as they relate to various aspects of imaging science such as radiation safety, radiation dose limits, patient and health professional protection, and patient positioning. Safety and high-quality image production are the goals of all who work within the imaging sciences. Therefore it is essential that students entering the health professions as medical imaging professionals understand the fundamental principles of physics.


The purpose of this chapter is to review the fundamentals of physics relevant to those considering medical imaging careers. In particular, it is a review of the behavior of matter under various conditions and an understanding of basic phenomena in our natural world. Mastery of these basic principles of physics is an integral step toward a career as a health professional in medical imaging.



Nature of Motion



Speed and Velocity


A study of the behavior of matter begins with understanding of the nature of motion. The most fundamental concept to comprehend is average speed. Average speed is defined as the distance an object travels divided by the time the object travels without regard to direction of travel. This concept is represented mathematically by the following equation, where vav= average speed, d = distance, and t = time:



image





Sample Problem



1. A car moves for 10 minutes and travels 5,280 meters. What is the average speed of the car?
A. 528 m/sec

B. 52.8 m/sec

C. 8.8 m/sec

D. 88 m/sec


Answer


C—Average speed is the distance an object travels divided by the time the object travels. First, the answers must be expressed in m/sec; therefore the time of travel by the car must be converted from minutes to seconds before the average speed is determined:



image



Dividing the distance traveled by the car (5,280 meters) by the new value for time traveled by the car (600 seconds) determines that the average speed of the car is 8.8 m/sec.



image



An important related concept is velocity. Velocity refers to speed in a specific direction. Speed is a scalar quantity (quantity described simply by a numeric value) and is expressed in units of magnitude. Velocity is a vector quantity (quantity describing the time rate of change of an object’s position) and must be expressed in both units of magnitude (i.e., speed) and direction of motion.


The average velocity of an object is determined by averaging the initial speed and the final speed of the object (add the two together and divide by 2). This concept is represented mathematically by the following equation, where vf = final velocity and vi = initial velocity.



image




Acceleration


Often, objects in motion change velocity over a period of time. Such a change in motion is called acceleration and is defined as the rate of change in velocity over a period of time. Acceleration is a vector quantity and is expressed in terms of magnitude and direction. This concept is represented mathematically by the following equation, where a = acceleration, vf = final velocity, vi = initial velocity, and Δt = the change in time.



image





Sample Problem



2. A cart is set in motion. The cart has an initial speed of 15 m/sec and moves for 25 seconds. At the end of 25 seconds, the cart’s speed is 40 m/sec. What is the magnitude of the cart’s acceleration?
A. 1.0 m/sec2

B. 2.2 m/sec2

C. 10.0 m/sec2

D. 1.1 m/sec2


Answer


A—Acceleration is determined by dividing the change in the cart’s velocity (final velocity [40 m/sec] – initial velocity [15 m/sec] = 25 m/sec) by the length of time the cart was in motion (25 seconds), indicating the cart is accelerating at 1.0 m/sec2.



image




Projectile Motion


The acceleration of objects released above the surface of the earth is influenced by the force of gravity. Gravity, assuming no wind resistance, accelerates an object released above the earth’s surface at a rate of 9.8 m/sec2. For example, if a rock is released from rest and falls toward the earth, the speed of the rock will increase by 9.8 m/sec for every second the object falls. At the end of 3 seconds the object will have a speed of 29.4 m/sec and a velocity of 29.4 m/sec in the direction toward Earth’s surface.


It is also possible for an object to display two types of motion simultaneously. This motion is generally called projectile motion. If a can is kicked from the edge of a cliff, the can will move horizontally at the same time it falls toward Earth (Figure 8-1). The horizontal motion is not an accelerated motion; therefore horizontal distance (dx) is a function of velocity (vx) and time (t) based on the following mathematic expression, where the x subscript is used to denote motion along the horizontal plane (x axis).


image

Figure 8-1 Projectile motion.



image



The vertical motion is more complicated. Gravity is acting vertically, so the velocity along the vertical plane (y axis) is constantly changing. The following mathematic expressions represent several methods of describing vertical motion, where vf = final velocity, vi = initial velocity, a = acceleration, d = distance, and t = time.



image





Sample Problem



3. A can is kicked off a cliff that is 19.6 m tall. The horizontal speed given to the can is 12.0 m/sec. Assuming there is no air resistance, how far out from the base of the cliff will the can land?
A. 12.0 m

B. 39.2 m

C. 6.0 m

D. 24.0 m


Answer


D—The problem provides values for the vertical distance (height of cliff), vertical acceleration (gravitational constant), and the initial vertical velocity (at rest on cliff, thus 0). The first step is to calculate time of flight. The following equation can be transformed to determine the time of flight.



image



vit drops out of the equation because the initial vertical velocity is 0.



image



Convert the equation to solve for time.



image



Once the time of flight is determined, insert the appropriate values into the horizontal distance equation to solve for horizontal distance.



image



Assuming no air resistance, the can will land 24.0 m from the cliff.



Newton’s Laws of Motion


Before delving into Newton’s laws of motion, a brief discussion of force is necessary. Force is defined as a push or pull on an object. When two forces are equal in magnitude and in opposing directions, they cancel each other out and result in a balanced force. However, if one of the two forces is greater than the other, then an unbalanced force exists and with it acceleration. Net force is simply the sum of the individual forces acting on an object. Keep in mind that the + and – signs are used to indicate direction of force and the mathematic rules associated with summing negative and positive numbers apply.



Newton’s First Law of Motion


Newton’s first law of motion states that a body at rest will remain at rest, and a body in motion will remain in motion with a constant velocity, unless acted on by an unbalanced force (a force not opposed by one of equal magnitude and in the opposite direction). Newton’s second law of motion states that an unbalanced force will cause acceleration, and this acceleration is directly proportional to the unbalanced force. This relationship is expressed mathematically as follows, where F = force, a = acceleration, and k = the constant of proportionality.



image




Newton’s Second Law of Motion


When used in Newton’s second law of motion, the constant of proportionality (k) is equal to the mass of the object. Therefore Newton’s second law is expressed mathematically as follows, where F = force, m = mass, and a = acceleration.



image





Sample Problem



4. A box rests on a tabletop. The box has a mass of 25 kg and is acted on by two forces. The force pushing to the right is 96 N, whereas the force pushing to the left is 180 N. Determine the magnitude of the acceleration of the box.
A. 11.0 m/sec2

B. 3.4 m/sec2

C. 5.5 m/sec2

D. 7.2 m/sec2


Answer


B—To determine the acceleration of the box, it is necessary to first determine the net force acting on the box. Remember that the net force acting on the box is simply the sum of all forces acting on the box. Because the two forces are opposing each other, one force is considered a positive force and the other a negative force. Therefore net force is represented by the following mathematic equation and is determined to be 84 N to the left.



image



Once the net force is determined, use Newton’s second law equation to determine the magnitude of acceleration of the box.



image



First, convert the formula to solve for acceleration.



image



The acceleration of the box is determined to be 3.4 m/sec2. note: Newtons are also expressed in kg-m/sec2.


If the mass is expressed in kilograms and the acceleration is expressed in meters per second squared (m/sec2), the unit of force is referred to as the newton (N) and is equal to the force necessary to accelerate a mass of one kilogram one meter per second per second. Weight is simply a specialized case of Newton’s second law. Weight can be stated mathematically as follows, where m = mass in kilograms and g = 9.8 m/sec2(i.e., the rate of acceleration associated with gravity).



image





Sample Problem



5. An object has a mass of 1,250 g. Determine the weight of the object on Earth.
A. 12,250 N

B. 122.50 N

C. 1,225.0 N

D. 12.25 N


Answer


D—To determine the weight of the object on Earth, first convert the units of mass to kilograms (1,250 g = 1.25 kg). Second, insert the appropriate values into the weight equation.



image



The weight of the object on Earth is determined to be 12.25 N.



Newton’s Third Law of Motion


Newton’s third law of motion states that for every action there must be an equal and opposite reaction.



Friction


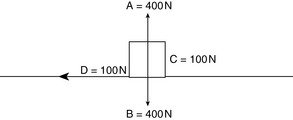
Friction is a force that opposes motion and is expressed in newtons. If a box (Figure 8-2) is slid on a surface at a constant rate by an applied force, we can deduce that friction is present and is opposing the motion of the box. Because there is no acceleration of the box, it is clear that friction is present and all forces are balanced. This relationship of balanced forces is represented in the diagram. Note that the normal force (A) and the weight (B) are balanced. The applied force (C) is to the right and has a magnitude of 100 N. The frictional force (D) is to the left and must also be 100 N if the box has no acceleration.


image

Figure 8-2 Depiction of a box being slid on a surface at a constant rate by an applied force.




Sample Problem



6. A crate is pulled to the right by a rope attached to the crate. The force applied to the rope is 600 N. As the crate slides along the floor, there is a frictional force between the crate and the floor that has a magnitude of 450 N. Determine the magnitude of the net force acting on the crate.
A. 1,050 N

B. 600 N

C. 150 N

D. 450 N


Answer


C—To determine the magnitude of the net force acting on the crate, remember that the magnitude of the net force acting on the box is simply the sum of all forces acting on the box. Because the two forces are opposing each other, applied force to the right and friction to the left, the magnitude of the net force is represented by the following mathematic equation and is determined to be 150 N to the right.



image




Rotation


In addition to displaying linear motion, an object may display a rotating or circular motion. The relationship between the angular displacement and the radius of the circle is expressed mathematically as follows, where θ = the angular displacement, s = arc length, and r = radius of the circle through which the object is moving.



image



The average speed of the circular motion can be described by looking at the number of rotations or revolutions an object makes in a given time. The angular speed is the number of radians completed in a given time unit. This is expressed mathematically as follows, where ω = angular speed, θ = the angular displacement, and t = time. When the mathematic expression is considered, it is important to remember that there are 2π radians in one revolution.



image



It is also possible to have an angular acceleration as a spinning or rotating object gains or loses speed. This is expressed mathematically as follows, where α = angular acceleration, ω = angular speed, and t = time.



image



The relationship between linear motion and rotational motion is analogous and conforms to Newton’s laws. Box 8-1 provides a description of the relationship between the mathematic expressions describing linear motion and those describing rotational motion. Beside each linear motion formula is its rotational motion counterpart. The expressions have been defined and applied within this chapter.



Box 8-1 Mathematic Expressions Describing Linear and Rotational Motion



image

Related posts:

  1. Reading Comprehension
  2. Anatomy and Physiology
  3. Chemistry
  4. Mathematics

Stay updated, free articles. Join our Telegram channel
Tags:
Apr 10, 2017 | Posted by in NURSING | Comments Off on Physics

Full access? Get Clinical Tree
Get Clinical Tree app for offline access