Pharmacology Math
Learning Objectives
1. Define, spell, and pronounce the terms listed in the vocabulary.
2. Apply critical thinking skills in performing patient assessment and patient care.
3. Summarize the important parts of a drug label.
4. Differentiate among the terms used in dosage preparation.
6. Demonstrate methods of verifying the accuracy of calculations.
7. Describe and perform conversions among the various systems of measurement.
8. Calculate the correct dose of a drug using the standard formula.
9. Determine accurate pediatric doses of medication.
10. Diagram how to reconstitute powdered injectable medications.
11. Specify the legal responsibilities of a medical assistant in calculating drug dosages.
Vocabulary
dispense To prepare a drug for administration.
nomogram Graph on which variables are plotted so that a particular value can be read on the appropriate line.
stat Immediately.
surface area The total area of the body exposed to the outside environment.
unit dose Method used by the pharmacy to prepare individual doses of medication.
Scenario
Heather Izacco, a recent graduate of a medical assistant program in the area, has just been hired by a local cardiologist, Dr. Angio. One of her responsibilities will be to administer medications under Dr. Angio’s supervision. Heather is confident of her ability to administer medications but is unsure of her accuracy in pharmacology math. Heather never did well in math at school and had a difficult time calculating accurate doses and converting between math systems during her medical assisting training. Her supervisor, Mrs. Allison, suggests that Heather review the math section of her textbook at home and be prepared to work out some sample problems next week.
While studying this chapter, think about the following questions:
• How can Heather be sure that she has calculated the correct dosages?
• What are the parts of a drug label and why are they important?
• Is it important that Heather be able to convert dosages from one system to another?
• What is the standard formula for determining the correct dose of a drug?
• Are there any differences between calculating an adult dose and calculating a pediatric dose?
• How would Heather go about reconstituting an injectable powder?
Medical assistants are responsible for being absolutely certain that the medication they prepare and administer to a patient is exactly what the physician ordered. Although drugs often are delivered by the pharmacy or supplied by pharmaceutical representatives in unit dose packs, the dosage ordered may differ from the dosage on hand. In this case, the medical assistant must be prepared to calculate the correct dose accurately before dispensing and administering the medication. There is never a margin of error in drug calculations, because even a minor mistake may result in serious complications for the patient. The medical assistant, therefore, must take meticulous care in calculating all drug dosages.
Drug Labels
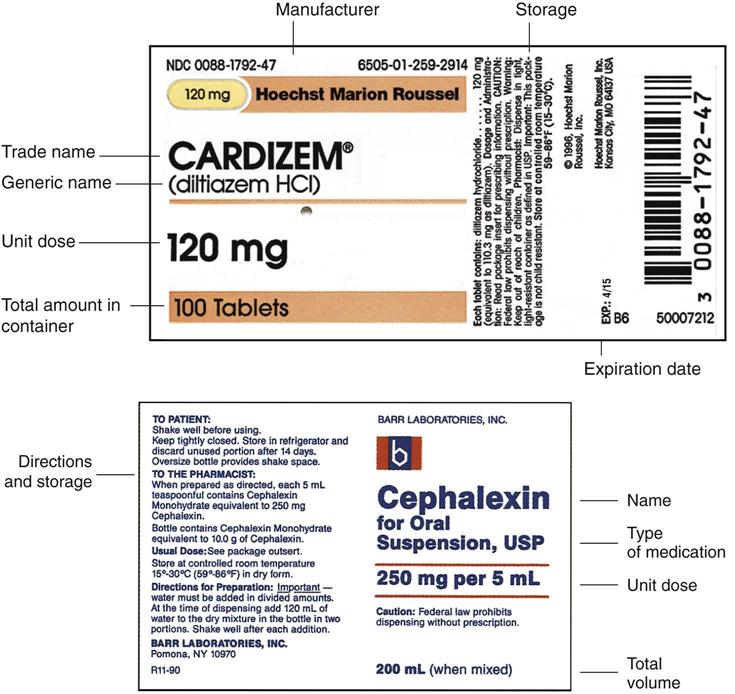
The first step in safely calculating a drug dosage is to accurately read the label of the drug on hand to determine whether the physician’s order and the packaged drug are in the same system of measurement. Starting at the top, the label shows the drug’s name with the brand name capitalized and typically in bold print. The brand name is copyright protected; therefore, it is followed by either a registered trademark (®) or trademark (™) symbol. The generic name is printed in lowercase letters under the brand name in smaller print. If a medication has been on the market for a long time, the generic name may be the only one listed (e.g., meperidine instead of Demerol, diazepam rather than Valium). If the medication is ordered from the pharmacy and stocked as a generic drug, only the generic name is printed on the label. In the label examples in Figure 34-1, Cardizem is the brand name of the generic drug diltiazem HCl; on the second label, cephalexin is the generic name for Keflex, and because copyright protection has ended, only the generic name is listed on the label.
Under the name of the drug, the dosage strength of the medication is given. Whether listed in milligrams (mg), milliliters (mL), or another unit of measure, the label states how much of the drug is contained in each of the identified units. This is what you must compare with the physician’s order to determine whether you must calculate the amount to administer to match the ordered dose of the drug. For example, the physician orders 250 mg of cephalexin, and the label states that the dosage strength is 250 mg per 5 mL; no calculation is needed—you simply administer 5 mL of the medication. However, if the physician orders 500 mg of the medication for a loading dose of the antibiotic, you must make sure you administer the correct amount of the medication to match the order. Sometimes the label helps by providing different but equivalent units of measurement for the dosage strength. For example, if the physician orders 250 mg of cephalexin and asks you to make sure the mother understands how much of the medication she should administer to her sick child, the label may state that 5 mL is equivalent to 1 teaspoon (according to the label, 250 mg of the drug is present in 5 mL of solution); therefore, you can confirm with the parent that the child should receive 1 teaspoon without having to do any calculation.
The label identifies the route, or method of administration, for the drug. If the medication is packaged as a tablet or a capsule, you can assume it should be given orally; liquid medication is labeled if it is for oral or parenteral use. If it is a powdered drug (solute) and it must be mixed with liquid (solvent) before administration, the label provides instructions on how to prepare the medication. Special storage precautions, such as light or heat sensitivity, are identified as well. At the bottom of the label is the total amount of the drug contained in the package. For example, a multidose bottle of cephalexin may contain as much as 200 mL of solution when mixed (e.g., 250 mg of cephalexin in each 5 mL of solution), and a single-dose bottle would contain one dose of the medication (250 mg in 5 mL of solution).
The name of the drug’s manufacturer appears on the label, as does an expiration date that must be checked each time the medication is dispensed. Dispose of all medications that have reached the label’s expiration date. The label also has a lot number stamped on the package so that it can be identified as belonging to a batch of drugs manufactured at the same time. This number becomes important if problems are noted with a particular batch and the medication is recalled. Depending on your employer’s preferences, you may need to include the lot number in the documentation of the medication on the patient’s chart. Finally, federal law requires that all labels have a national drug code (NDC) that identifies that particular drug.
Some of the basic information provided on drug labels includes the following:
Math Basics
You may need to review some basics of arithmetic before you tackle drug calculations. You must thoroughly understand the addition, subtraction, multiplication, and division of fractions and decimals; the relationship of decimals and fractions; and how they are converted from one to the other.
Fractions
A fraction is a part of a whole, that is, fractions are a way of dividing a whole unit into parts. For example, think of dividing a small cherry pie into equal parts for friends after dinner. Four people want dessert, so you can divide the pie into four equal parts; each person receives 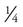 of the pie. If only three people want dessert, you can divide the pie into three equal parts; each person receives
of the pie. If only three people want dessert, you can divide the pie into three equal parts; each person receives 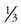 of the pie.
of the pie.
The top number in a fraction is the numerator, and the bottom number is the denominator. In a proper fraction, the numerator is smaller than the denominator. If we go back to the pie example, 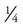 and
and 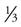 of the pie are proper fractions.
of the pie are proper fractions.
In improper fractions, the numerator is equal to or greater than the denominator. Another way of looking at improper fractions is that the numerator is so large that it is equal to or greater than 1. For example, the improper fraction 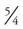 is greater than 1. It is equal to
is greater than 1. It is equal to 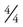 (the entire pie that was cut into 4 pieces, or 1 whole pie) plus
(the entire pie that was cut into 4 pieces, or 1 whole pie) plus 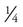 of another pie. Therefore, if you wanted everyone to have
of another pie. Therefore, if you wanted everyone to have 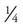 of a pie for dessert, you would need two pies: one whole pie for four guests (
of a pie for dessert, you would need two pies: one whole pie for four guests (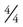 ) and
) and 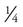 of another pie for yourself (
of another pie for yourself (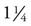 pies). To convert improper fractions into whole numbers, divide the numerator by the denominator. In this case, you need
pies). To convert improper fractions into whole numbers, divide the numerator by the denominator. In this case, you need 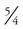 of pie: 5 + 4 =
of pie: 5 + 4 = 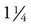 pies.
pies.
Review the following examples. Identify the proper and improper fractions. If the fraction is improper, perform the math to get the whole number equivalent.
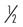 | _______________ | 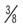 | _______________ |
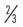 | _______________ | 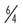 | _______________ |
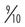 | _______________ | 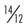 | _______________ |
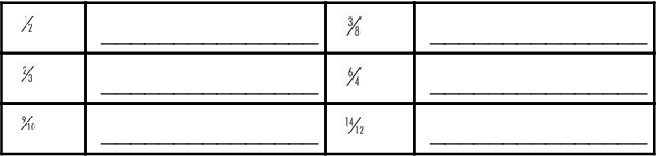
Fractions typically are written in their lowest terms. For example, can you reduce the fraction 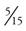 to its lowest term? To reduce a fraction, you must divide the numerator and the denominator by the largest number that goes into each equally. In the case of
to its lowest term? To reduce a fraction, you must divide the numerator and the denominator by the largest number that goes into each equally. In the case of 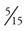 , 5 divides into 15 three times, which means that
, 5 divides into 15 three times, which means that 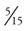 can be reduced to
can be reduced to 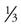 . Other examples include the following:
. Other examples include the following:
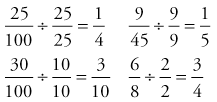
In some cases, you may have to multiply fractions. For example, let’s say you want to multiply 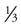 of the contents of one bottle times
of the contents of one bottle times 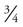 of the contents of another. All you have to do in this case is multiply the numerators and denominators of each fraction and reduce the answer to its lowest terms. For example:
of the contents of another. All you have to do in this case is multiply the numerators and denominators of each fraction and reduce the answer to its lowest terms. For example:
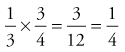
To divide fractions, you must invert the divisor (the second fraction) before you multiply the numerators and denominators. For example:
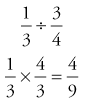
Decimals
A decimal is similar to a fraction, but it is expressed in units of tenths (0.1), hundredths (0.01), and thousandths (0.001). To perform drug calculations, fractions first must be converted into decimals. To convert a fraction into a decimal, simply divide the numerator by the denominator. For example, rather than ordering ¾ of a dose for a patient, the physician orders the decimal equivalent. To perform this math, you may need to add zeroes after the decimal point at the end of the numerator.
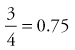
If the answer is less than a whole number, it is crucial to place a zero before the decimal point to prevent a medication error. For example, if you are to administer .5 mL of a medication and the zero is not placed before the decimal point, you may miss the decimal point and think that the correct dose is 5 mL. Also, a zero should never be placed after the decimal point of a whole number. Mathematically, a whole number such as 1 mL is actually 1.0 mL. However, if the decimal point and a zero follow the whole number, the dose may be misinterpreted as 10 mL.
Percent
A percent is a number expressed as part of 100. Decimal numbers can be converted to percentages by dividing the number by 100 or by simply moving the decimal point two spaces to the right. For example:
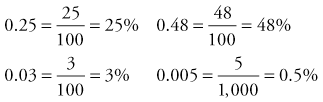
Ratio and Proportion
A ratio is one way of expressing a fraction or a division problem; it shows the relationship of the numerator to the denominator. The comparison of two ratios is called a proportion. A proportion is written as follows:
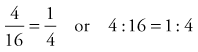
This is read as 4 divided by 16 equals 1 divided by 4, or 4 is to 16 as 1 is to 4. The physician’s order for a medication may be a ratio different from that of the medication in stock. To determine the correct proportion for administration, the ordered ratio must be compared with the available ratio (what is in stock).
The preceding proportion example has all the answers in it; there is nothing to solve. In calculating dosages, mathematical proportions are used, but with one element unknown. We must solve for that unknown, or x. For example:
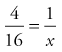
Always in a proportion, the problem is solved by cross-multiplication. Do not confuse this with plain multiplication. An equals sign (=) between two fractions indicates that this is an equation to be cross-multiplied.
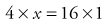
therefore, 4x = 16.
We know what 4x equals, but next we must find what 1x, or x, equals. To find the value of x, we must find a way to leave x (or 1x) alone on the left side of the equation. We can change 4x to 1x by dividing the number 4 by itself:
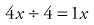
However, what we do on one side of an equation, we must do on the other side, or the equation will not be equal anymore. Therefore, we also divide 16 by 4:
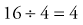
therefore, x = 4 and 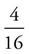 =
= 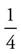 .
.
Another way to make sure your proportion answer is correct is to check your answer by multiplying the means (the middle numbers of the equation) and the extremes (the outer numbers of the equation). If your answer is correct, multiplication of the means and extremes produces answers that are equal. For example:
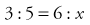
If the problem is solved by cross-multiplication, the equation looks like this:
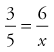
After cross-multiplying, we have:
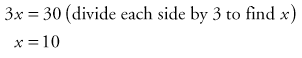
therefore, our equation is 3 : 5 = 6 : 10.
To check the accuracy of your equation, multiply the means (5 × 6 = 30) and the extremes (3 × 10 = 30). Because the answers are equal, you know you have the correct proportion. Table 34-1 provides some examples of the relationships between percents, decimals, fractions, and ratios.
TABLE 34-1
| PERCENTAGE | DECIMAL | FRACTION | RATIO |
| 25 | 0.25 | ¼ | 1 : 4 |
| 50 | 0.5 | ½ | 1 : 2 |
| 60 | 0.6 | 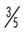 ( (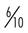 ) ) | 3 : 5 |
| 0.5 | 0.005 | 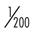 | 1 : 200 |
| 0.1 | 0.001 | 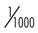 | 1 : 1,000 |
| 85 | 0.85 | 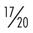 | 17 : 20 |
| 1 | 0.01 | 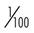 | 1 : 100 |
Determine the following equivalents:
| 0.20 | = _____ (percent) | = _____ (fraction) | = _____ (ratio) |
| 37% | = _____ (decimal) | = _____ (fraction) | = _____ (ratio) |
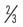 | = _____ (ratio) | = _____ (percent) | = _____ (decimal) |
| 3 : 4 | = _____ (fraction) | = _____ (decimal) | = _____ (percent) |

Rounding Calculations
What should you do if the dose of the supplied drug does not exactly match your calculation? For example, what if you calculate a tablet dose as 1.75 tabs, but you have only whole tablets available? First, check your calculation for accuracy, then check the stocked supply of the drug to make sure no other dosages are available. If the calculation is correct and no other dosages of the drug are available, you will have to round your answer to the nearest amount that matches the dose available. If the calculation is 0.5 or greater, round up to the next whole number. For 1.75 tablets, 0.75 would be rounded up to 1, and the patient should be given two tabs of the medication. However, make sure you check with the physician before administering a rounded dose of medication.
Determine the correct doses for the following examples:
| 1.2 tabs = _______ tablet(s) | 1.55 tabs = _______ tablet(s) |
| 1.37 tabs = _______ tablet(s) | 0.56 tab = _______ tablet |
| 1.64 tabs = _______ tablet(s) | 0.81 tab = _______ tablet |
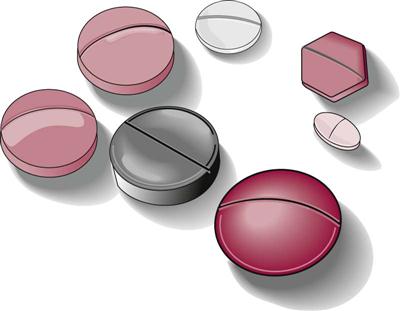
Some tablets are scored, which means that the medication was manufactured with an impression or groove down the center of the tablet. This type of tablet can be accurately divided into two equal parts; therefore, calculations can be rounded to the closest half-tab (Figure 34-2). For example, 0.4 tab would be rounded up to one-half of a scored tab, and 1.7 tabs would be 2 tabs. Never give a partial dose of a tablet unless the tablet has been scored, and then the dose can be given rounded to the nearest ½.
If a liquid medication is to be administered, it usually is acceptable to round the dose to the nearest tenth. For example, if the correct calculation for an injection of an antibiotic is 1.46 mL, administer 1.5 mL of the drug (the calculation is greater than 0.05). The exceptions to this rule are (1) pediatrics, because accurate doses for children may be much smaller than adult doses; and (2) if the dose is less than 1 mL and the syringe you are using is calibrated in hundredths, the medication is rounded to the nearest hundredth. What are the correct doses of the following medications, rounded to the nearest tenth?
| 1.47 cc = _______ cc | 1.33 mL = _______ mL |
| 2.62 mL = _______ mL | 2.15 cc = _______ cc |
| 1.08 mL = _______ mL | 1.15 mL = _______ mL |
Systems of Measurement
If the dosage ordered by the physician is different from the dosage on hand, the medical assistant must follow three basic steps to calculate the prescribed dose accurately:
2. Perform the calculation in equation form using the appropriate formula.
3. Check your answer for accuracy and ask someone you trust to confirm your calculations.
All three steps must be completed before the medication is dispensed and administered. Confirm your calculations with the physician if you have any doubt of their accuracy.
Sometimes the physician orders a medication in a strength completely different from the one on the drug label. For example, the physician may order 1 gr (grain) of a drug, but the available dosage form is in milligrams. Before the medical assistant can use the ratio and proportion formulas to arrive at the amount to administer, he or she first must convert to one system or the other. The medical assistant must convert the ordered dose to the measurement system on the drug label (i.e., what is available), because that system must be used to dispense the drug.
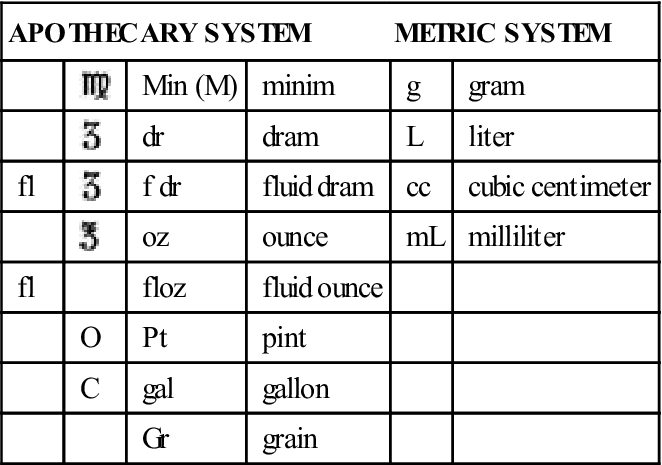
Three different systems of measurement are used for medications: the metric system, the apothecary system, and the household system. Table 34-2 presents abbreviations and symbols used in the apothecary and metric systems.
TABLE 34-2
Abbreviations and Symbols for Selected Weights and Measures
| APOTHECARY SYSTEM | METRIC SYSTEM | ||||
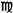 | Min (M) | minim | g | gram | |
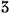 | dr | dram | L | liter | |
| fl | 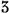 | f dr | fluid dram | cc | cubic centimeter |
 | oz | ounce | mL | milliliter | |
| fl | fl oz | fluid ounce | |||
| O | Pt | pint | |||
| C | gal | gallon | |||
| Gr | grain | ||||
Metric System
The metric system of weights and measures is used throughout the world as the primary system for weight (mass), capacity (volume), and length (area). In the United States, the metric system is used for scientific work, including most tasks involving pharmaceuticals. However, some medication forms still use the older apothecary system; therefore, the medical assistant must learn the two systems and the relationships (conversions) between them.
The metric system of weights and measures is a decimal system based on the number 10, and all calculations are completed by moving decimal points to the right or to the left. Each higher measure is 10 times the measure at hand; each lower measure is 0.1 (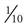 ) the measure. The basic units are multiplied or divided by units of 10. The fraction is always written as a decimal, and the number precedes the letters designating the actual measure. Thus 1½ liters would be written 1.5 L. The cubic centimeter (cc) and the milliliter (mL) are interchangeable; however, the Joint Commission (formerly the Joint Commission on Accreditation of Healthcare Organizations [JCAHO]) advises against the use of the cc abbreviation in documenting medications in the patient’s record.
) the measure. The basic units are multiplied or divided by units of 10. The fraction is always written as a decimal, and the number precedes the letters designating the actual measure. Thus 1½ liters would be written 1.5 L. The cubic centimeter (cc) and the milliliter (mL) are interchangeable; however, the Joint Commission (formerly the Joint Commission on Accreditation of Healthcare Organizations [JCAHO]) advises against the use of the cc abbreviation in documenting medications in the patient’s record.
In the metric system, 1 cc is a measurement of area, and an area this size holds exactly 1 mL, or 0.001 (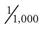 ) of a liter of fluid. The milliliter measures the amount of liquid medication, or the volume, that is to be given orally or by injection. The gram (g) measures the weight, or strength, of a solid medication, such as a tablet, powder, or topical preparation. The meter is the measurement for length in the metric system. A meter is equal to 39.37 inches, which is slightly longer than a yard, or 3.28 feet. One inch is equal to
) of a liter of fluid. The milliliter measures the amount of liquid medication, or the volume, that is to be given orally or by injection. The gram (g) measures the weight, or strength, of a solid medication, such as a tablet, powder, or topical preparation. The meter is the measurement for length in the metric system. A meter is equal to 39.37 inches, which is slightly longer than a yard, or 3.28 feet. One inch is equal to 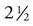 centimeters (cm). The medical assistant may use centimeter measurements when measuring the depth and borders of a wound.
centimeters (cm). The medical assistant may use centimeter measurements when measuring the depth and borders of a wound.
The units of measurement in the metric system are based on their prefixes: kilo– means 1,000, and milli– means 0.001. The prefixes mean the same whether used to measure volume or weight. For example, a kilogram (kg) is 1,000 grams (g), and a kiloliter (kL) is 1,000 liters (L); a milligram (mg) is 0.001 (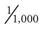 ) of a gram, and a milliliter (mL) is 0.001 (
) of a gram, and a milliliter (mL) is 0.001 (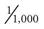 ) of a liter.
) of a liter.
Conversions within the metric system may be necessary if the physician orders a unit that is different from the one on the drug label. Units in the metric system are converted by moving the decimal point in multiples of 10. When larger units of measurement are converted to smaller ones (e.g., grams to milligrams), the answer is a larger number, so the decimal point is moved three places to the right (0.35 g = 350 mg). When smaller units of measurement are converted to larger ones, the answer is a smaller number, so the decimal point is moved three places to the left (e.g., 150 mL = 0.15 L). The following equivalents can be used to make conversions within the metric system.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


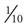 of a gram
of a gram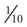 of a liter
of a liter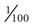 of a gram
of a gram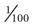 of a liter
of a liter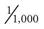 of a gram
of a gram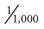 of a liter
of a liter