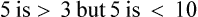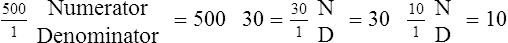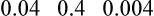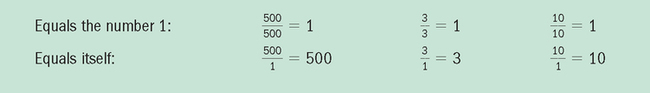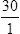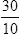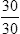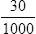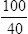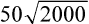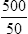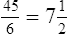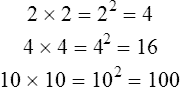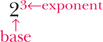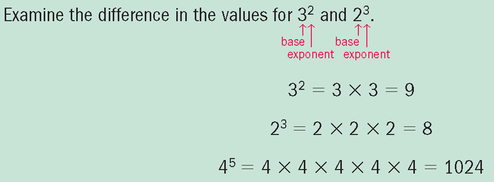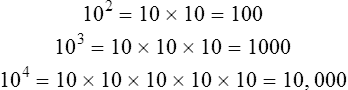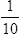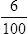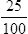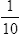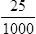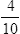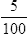• Define and interpret the symbols and vocabulary of basic mathematics. • Insert leading zeros and eliminate trailing zeros. • Calculate sums, products, and multiples of numbers. • Identify factors and multipliers. • Calculate squares and square roots. • Use mental arithmetic to calculate powers of base 10. • Read, write, multiply, divide, and round decimal numbers. • Add, subtract, multiply, cancel, divide, and reduce simple, mixed, and improper fractions. • Compare fraction size by creating equivalent fractions. • Convert fractions, decimal numbers, and percents. • Estimate and evaluate answers. • Skim the chapter objectives. • Skim each topic in the chapter. • When more review of a topic is needed, take the designated Rapid Practice quiz for that topic. • The depth of your review depends on your assessment of your comprehension. A review before taking a test boosts scores. • Be sure you can answer all of the questions provided. • Revisit any content areas where questions are missed. • When your review is completed, take the Multiple-Choice Review and the Chapter 1 Final Practice. • Refer to a basic mathematics text if further explanation is needed. 1. A blood pressure goal for healthy adults is ≤120/80. 2. If the pulse is <50, notify the physician. 3. When a blood pressure is ≥120/80 in an otherwise healthy adult, lifestyle changes need to be instituted. 4. According to the Centers for Disease Control and Prevention (CDC), one of the characteristics of SARS disease is a temperature >100.4°F (38°C). 5. Identify the symbol used for square root. 1. Inject the medicine in the baby’s thigh if he has walked ______ a year. (less than) 2. Give the patient 1 teaspoon of medicine if his age is _______ 5 years. (less than or equal to) 3. The risk of cancer from smoking is greatly accelerated when the patient has a history of smoking ______ 20 years. (greater than or equal to) 4. If the systolic blood pressure is _______ 180, notify the physician. (greater than) 5. The _________ symbol is used in medication math to determine body surface area for safe dosages for very powerful medicines. (square root) Implied decimal points, if written, can be misread as commas, zeros, or the number one. The square root symbol (√) is used to reduce writing and increase comprehension: To obtain a square root on a calculator, enter the number followed by the square root symbol. 1. Which is a common factor of the numbers 8 and 10? ______ 2. Which is a multiple of 36? ______ 3. What is the square of 4? ______ 4. Which is the multiplier of 8 ×¼? ______ 5. What is the square root of 25? ______ • To divide, examine the divisor—10, 100, or 1000—for the number of zeros. In the dividend, move the decimal point (real or implied) to the left by a number of places that is equal to the number of zeros: • To multiply, examine the multiplier—10, 100, or 1000—for the number of zeros. In the number being multiplied, move the decimal point to the right by a number of places that is equal to the number of zeros: Insert zeros in front of decimals, and avoid trailing zeros after whole numbers. 1. 30 multiplied by 100 = ______. 2. 0.4 multiplied by 1000 = ______. 3. 5000 divided by 100 = ______. 4. 250 divided by 1000 = ______. 5. 1500 divided by 100 = ______. Fractions with denominators other than powers of 10 are covered in more detail on p. 23. Read the number to the right of the decimal point as the numerator. Write the number or numbers that appear to the right of the decimal point as the numerator. Write the power of 10 (e.g., 10, 100, or 1000) according the decimal places in the denominator. The number of zeros in the denominator is equal to the number of decimal places.
Essential Math Review
Directions
Essential Math Vocabulary and Concepts
Read
Write
Example
<
Less than
The baby weighs < 5 pounds.
>
Greater than
The total cholesterol was high (> 200).
≥
Greater than or equal to
Give the medications if the systolic blood pressure ≥ 160.
≤
Less than or equal to
Hold the medication if his temperature is ≤ 100.
√
Square root
√16 means the square root of 16.
Implied Decimal Points and Trailing Zeros
![]() Do not remove zeros that occur within a number. The number 3.08 would be read as 3.8 if this error was made, resulting in a tentimes error.
Do not remove zeros that occur within a number. The number 3.08 would be read as 3.8 if this error was made, resulting in a tentimes error.
![]() Do not remove zeros that occur before a decimal point. They alert the reader to a decimal that follows the zero immediately:
Do not remove zeros that occur before a decimal point. They alert the reader to a decimal that follows the zero immediately:
![]() Always place a zero in front of a decimal point that is not preceded by a whole number.
Always place a zero in front of a decimal point that is not preceded by a whole number.
![]() Always eliminate implied decimal points and trailing zeros that follow a whole number. Implied decimal points and trailing zeros do not change the value, but they do lead to reading errors and medication dosage errors.
Always eliminate implied decimal points and trailing zeros that follow a whole number. Implied decimal points and trailing zeros do not change the value, but they do lead to reading errors and medication dosage errors.
Factor
![]() A factor can only be less than or equal to a given whole number. One and the number itself are always factors. “Factoring” the number 9 gives you 1, 3, 9.
A factor can only be less than or equal to a given whole number. One and the number itself are always factors. “Factoring” the number 9 gives you 1, 3, 9.
![]() Factor also has other meanings. It also can be used as a general term to describe relevant data. For example, “He examined all the factors in the case” or “A dimensional analysis equation permits all the factors to be entered in one equation.”
Factor also has other meanings. It also can be used as a general term to describe relevant data. For example, “He examined all the factors in the case” or “A dimensional analysis equation permits all the factors to be entered in one equation.”
Square Root
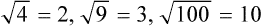
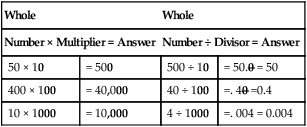
Multiplying and Dividing by 10, 100, and 1000
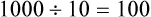
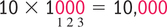
![]() Whenever there are more than four numbers in a group, insert a comma in front of every three digits from right to left to ease the reading: e.g., 1000000 becomes 1,000,000 (1 million), and 20000 becomes 20,000 (20 thousand).
Whenever there are more than four numbers in a group, insert a comma in front of every three digits from right to left to ease the reading: e.g., 1000000 becomes 1,000,000 (1 million), and 20000 becomes 20,000 (20 thousand).
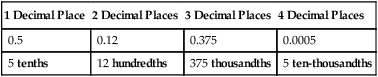
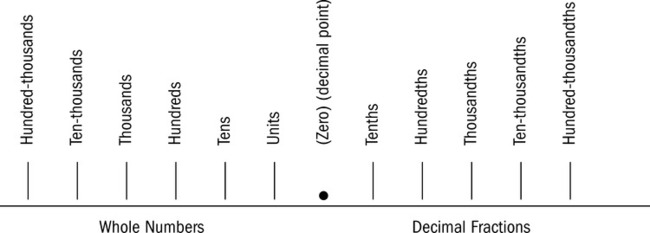
Decimal Fractions
![]() Decimals replace the division bar and the denominator of a fraction with a decimal point in the specified place that identifies power of 10 in the denominator. Zeros are used to hold the place values.
Decimals replace the division bar and the denominator of a fraction with a decimal point in the specified place that identifies power of 10 in the denominator. Zeros are used to hold the place values.
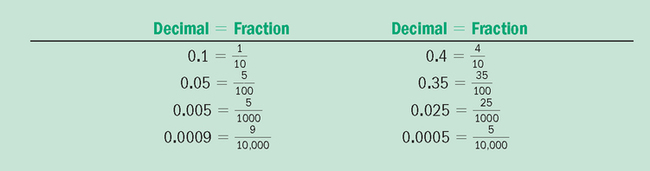
Writing Decimals in Fraction Form
![]() Insert leading zeros before decimal points and remove trailing zeros. Commas, decimal points, and the number 1 must be distinguished to avoid errors.
Insert leading zeros before decimal points and remove trailing zeros. Commas, decimal points, and the number 1 must be distinguished to avoid errors.
![]() To avoid 10, 100, and 1000-fold errors, the decimal point must be clearly identified and in the correct place:
To avoid 10, 100, and 1000-fold errors, the decimal point must be clearly identified and in the correct place:
Essential Math Review
Get Clinical Tree app for offline access