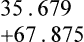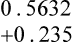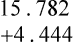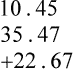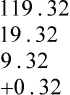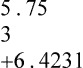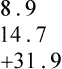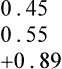Upon completion of this chapter, the learner will be able to: 1. Define the key terms that relate to word problems, percentages, and decimals. 2. Identify key terms within a word problem and compute the problem with 100% accuracy. 3. Identify situations that benefit from using percentages and decimals in health care professions. 4. Manipulate decimal computations with 100% accuracy. 5. Manipulate percentage computations with 100% accuracy. 6. Convert numbers between their fraction, decimal, and percentage forms with 100% accuracy. What is it about word problems that gives people the most difficulty? When I ask this question in class, the most common answer is, “I’m so worried about the numbers that I miss the key words in the problems.” Most of the time, we do not communicate by writing math problems. We use words to describe the relationship between the numbers and the information we are trying to obtain (Boxes 4-1 and 4-2 and Table 4-1). TABLE 4-1 Key Phrases for One or More Computations Use the steps in the box Strategy 4-1 to solve the following word problem: Kevin spends a total of $30.00 for lunch during a 5-day workweek. What is the average amount he spends on lunch each day? Solution for the example question: 2. Underline what the question is asking. 3. Identify what you are trying to find. 4. Pull out important information in the problem. a. Kevin spends a total of $30.00 for lunch in a 5-day workweek. b. What is the average amount Kevin spends on lunch each day? 5. Identify the mathematical operation necessary to answer the question. 6. Perform the mathematical calculation accurately. 8. Check to make sure the answer satisfies the question that was asked in the problem. 9. Ensure that the answer makes sense. Solution for the example question: 2. Underline what the question is asking. 3. Identify what you are trying to find. 4. Pull out important information in the problem. 5. Identify the mathematical operation necessary to answer the question. a. Determine the total cost of each supply b. Add the total cost of each supply to obtain the grand total of the order. 8. Check to make sure the answer satisfies the question that was asked in the problem. 9. Ensure that the answer makes sense. The same strategy used for rounding whole numbers can be used for rounding decimals. Refer to the box Strategy 4-2 when completing the Practice the Skill problems that follow it. 1. Identify the place value to which you are rounding. Identify the hundredths place: 3.4567 2. Look to the immediate right (one place value) of the place value you are rounding. 3. If this number is 5 or greater, round the place value up by one digit and drop all the remaining numbers to the right. If you are having difficulties with this section, review the concept of rounding numbers in Chapter 2 (p. 34).
Word Problems, Percentages, and Decimals
Objective 2
Understanding word problems
Key Phrase
Operation
What is the total?
Addition
What is the average?
Addition and division
What is the total cost?
Addition
What is the discount?
Multiplication
What are the hidden charges?
Depending on how the problem is worded, involves addition and subtraction
What is the total discount?
Depending on how the problem is worded, involves multiplication, addition, or subtraction
Objective 2
How to solve a word problem
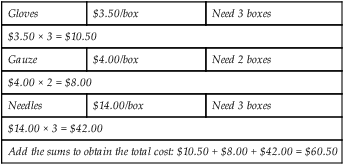
Gloves
$3.50/box
Need 3 boxes
Gauze
$4.00/box
Need 2 boxes
Needles
$14.00/box
Need 3 boxes
Gloves
$3.50/box
Need 3 boxes
$3.50 × 3 = $10.50
Gauze
$4.00/box
Need 2 boxes
$4.00 × 2 = $8.00
Needles
$14.00/box
Need 3 boxes
$14.00 × 3 = $42.00
Add the sums to obtain the total cost: $10.50 + $8.00 + $42.00 = $60.50
Objectives 3, 4
Decimals
Example:
Round 3.4567 to the nearest hundredth.
Thus, your answer is 3.46.

Word Problems, Percentages, and Decimals
Get Clinical Tree app for offline access

 MATH IN THE REAL WORLD 4-1
MATH IN THE REAL WORLD 4-1 STRATEGY 4-1
STRATEGY 4-1 PRACTICE THE SKILL 4-1
PRACTICE THE SKILL 4-1 STRATEGY 4-2
STRATEGY 4-2 HUMAN ERROR 4-1
HUMAN ERROR 4-1 PRACTICE THE SKILL 4-2
PRACTICE THE SKILL 4-2 STRATEGY 4-3
STRATEGY 4-3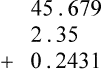
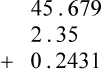

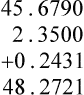

 PRACTICE THE SKILL 4-3
PRACTICE THE SKILL 4-3