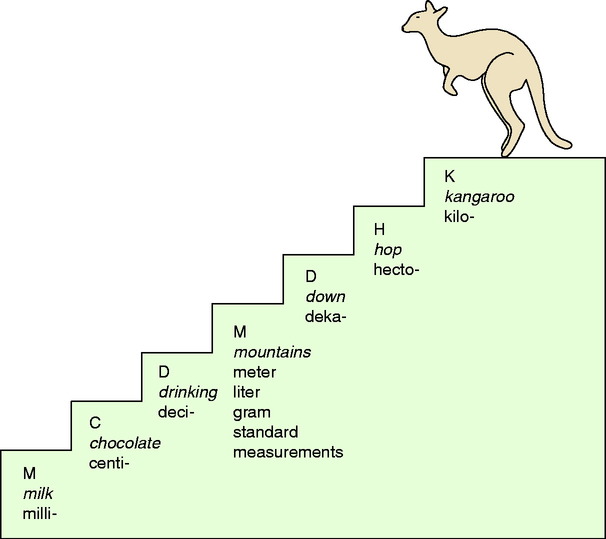
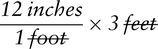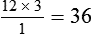Upon completion of this chapter, the learner will be able to: 1. Define the key terms that relate to the chapter. 2. Identify the key prefixes and word roots related to the metric system. 3. Convert between base unit metric measurements with 100% accuracy. 4. Convert between basic metric mass and volume measurements with 100% accuracy. 5. Solve proportional problems using dimensional analysis theory. 6. Calculate mass and volume medication problems with 100% accuracy. Many of us have been exposed to the metric system since grade school. Through the years, knowledge of the metric system has become necessary in the fields of engineering, steel production, the automotive industry, and health care. The health care industry in the United States uses a combination of the metric system, household measurements, and the apothecary system in dispensing medications and educating patients about their medications. In this chapter, we focus on the metric system and common metric conversions. Meter (M, m) is used to describe length. Liter (L) is used to describe volume. (The abbreviation for liter is always capitalized to avoid misinterpretation as the number 1.) The following is a list of the prefixes used in the metric system and their meanings: It is important to memorize these terms and the amounts they represent. A common mnemonic used to remember the prefix order from largest measurement to smallest is: Kangaroo Hop Down Mountains Drinking Chocolate Milk (Figure 7-1). Example: A patient drank 250 ml at breakfast, 500 ml at lunch, and 525 ml at dinner. How much did the patient drink during his meals on this day? The correct answer is 1275 ml. There are many ways to convert measurements in the metric system in order to determine equivalent measurements. In this chapter, we use the proportion and cross multiplication strategies learned in Chapter 5 and dimensional analysis. Let’s take a quick moment to review the steps for writing a proportion. 2. Identify the known information. 3. Write your proportion so that the same units appear in the same location for each proportion. 4. Solve the problem using cross multiplication if your proportion is written as a fraction. If the problem is written in linear fashion, multiply the means (“inside” numbers) together and the extremes (“outside” numbers) together. 1. Establish what information is known. 2. Determine what is the known equivalent or conversion for which the problem is asking. 3. Write down what is known on the left side of the equation. 4. Write down the remaining known information on the right side of the equation. 5. Identify the unknown information with an “X” in the equation. 6. If possible, reduce fractions before cross multiplication. 7. Cross multiply and solve for the unknown as learned in Chapter 5. To use dimensional analysis concept, you must find the answers to three questions:
The Metric System
Objective 1
Objective 2
Prefixes and base units (word roots)
Kilometer
Kilo- is the prefix
Meter is the base word
Milliliter
Milli- is the prefix
Liter is the base word
Microgram
Micro- is the prefix
Gram is the base word
Objectives 3, 4, 5
Conversion of measurements in the metric system
Example:
How many meters are in 3,000 mm?
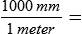
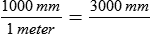
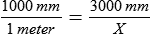
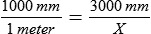
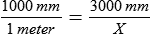
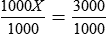
Check your answer by substituting 3 for “X” and solving the problem.

Objective 5
Dimensional Analysis

![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


The Metric System
Get Clinical Tree app for offline access

 MATH TRIVIA 7-1
MATH TRIVIA 7-1 Human Error 7-1
Human Error 7-1 STRATEGY 7-1: Documentation
STRATEGY 7-1: Documentation MATH ETIQUETTE 7-1
MATH ETIQUETTE 7-1 PRACTICE THE SKILL 7-1
PRACTICE THE SKILL 7-1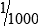
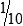
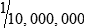
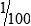
 STRATEGY 7-2: Solving Equivalency Problems
STRATEGY 7-2: Solving Equivalency Problems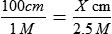
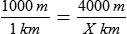
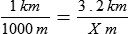

 STRATEGY 7-3: Dimensional Analysis
STRATEGY 7-3: Dimensional Analysis