13. Statistics in research
Key points



 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

• Collecting quantitative data means that statistical processes will be involved in the analysis stage. Understanding the principles behind these processes is important in correctly interpreting the findings of research.
• Research findings are presented following certain conventions and use presentation methods such as tables, bar charts, histograms and pie charts. Every picture tells a story, so these should never be overlooked.
• Statistics fall into two main categories of descriptive and inferential. Users of research need to know the principles and assumptions on which these are based as well as those relating to parametric and non-parametric tests.
• The level of measurement of the data will influence many of the decisions made in the research process. An understanding of these levels is crucial to understanding why certain decisions are made in the choice of statistical techniques.
• Although the jargon and symbols used in statistics may look intimidating, in reality a basic understanding is not difficult to achieve. Competency in understanding basic statistical principles is essential to applying research to evidence-based practice.
This is the chapter you may be tempted to skip; however, do not pass on just yet. Understanding the way numbers are presented in research is one of the most important skills that will help you in making sense of research articles. It is also an essential chapter if you have to present your own quantitative findings in research or audit. To read research papers in greater depth, every midwife needs to understand some of the key statistical principles that will help in deciding in quantitative research whether the author’s conclusions are justified. So, although it is easy to ignore the statistical sections in research, understanding them can have a direct effect on care. Indeed,Spiby and Munro (2010)suggest that if midwives are to integrate evidence-based practice into their care, they must understand research and be able to interpret the data on which it is based.
The aim of this chapter is to explain just some of the common statistical ideas used in quantitative research, the basic principles underpinning them, and how to interpret them.
Common attitudes to statistics
Once quantitative researchers have gathered the data from their study, they are faced with transforming the raw results into some kind of order that can be understood. Any summary and presentation of the data will involve numbers and statistical processes and this is where the problems can start. For many people, the way numbers are presented and the statistical techniques applied to the data creates problems, and is the point at which some readers decide either to ignore the numbers, or put down the article.
Why do statistics make so many people turn cold? Perhaps they remind us of unpleasant experiences in school where we felt lost or left behind. For some, the easiest way of coping with these feelings is to give up, and pretend statistics do not matter. Unfortunately, they do. For those ready to make a fresh start, this chapter will explain just a small selection of some of the statistical procedures you will meet in many research reports. You will not have to learn how to carry out complicated calculations; there are specialised books and courses that will help you if you need to know this. For those carrying out research there are also people with this expertise to draw on, but you do have to know what to ask.
If the very word ‘statistics’ frightens you, let us start by acknowledging that without statistics the results of any study would just be a chaotic jumble of numbers that would provide little meaning (Polit and Beck 2008). Statistical processes bring order and understanding to all the information that has been collected.
As with research in general, there are some unusual words and symbols to learn and some familiar words that have different meanings (see Table 13.1). One example is the word ‘significant’. This does not mean ‘important’, but suggests that the difference in the outcomes between two groups in, say, a randomised control trial (RCT), is unlikely to have happened by chance. In other words, the difference between the two groups is more likely to be explained by what the researcher did than by any other explanation. For this reason, when talking or writing about research, unless you are using it in its statistical sense, it is better to avoid saying something is ‘significant’. Similarly, the word ‘data’ is plural, so you will see the word ‘are’ not ‘is’ following it, as well as expressions such as ‘the data were calculated’, not ‘was’ calculated.
| Symbol | Meaning | Use |
|---|---|---|
| Σ | Greek symbol meaning add together what follows | As part of a formula providing instructions, e.g. Σx, which means add together each value for the variable collected. |
| < | Less than | Indicates set value e.g. P<0.05 means that the value of P is below or smaller than 0.05. |
| > | Greater than | Indicates the opposite of the above as in P>0.05, which means that the value is greater than 0.05. The open end of the symbol means greater than, and the closed end means less than reading from the left hand side of the symbol. |
| ≥ | Equal to or greater than | To indicate a condition to be met during a calculation. |
| ± | Plus and minus the figure that follows | Used for example in standard deviation (sd) where the figure that follows the symbol is taken away from the mean and then added to the mean to give the range between which the majority of values in the data set will fall. |
| χ2 | Symbol for the chi-squared test (pronounced ‘ki-squared’) as in kite | This test indicates the chances that any differences between the groups in the study could have happened by chance. The test is used with ‘nominal data’ (i.e. falling into one category or another, such as yes or no) and compares the actual results with what might have been expected if there was no difference between the groups. |
| p<0.05 | Used as part of statistical tests to indicate the level of probability of being wrong if a real difference between the groups involved was assumed | This is the minimum level set for tests of significance to indicate that the results are unlikely to have happened purely by chance. Roughly, it means you would be wrong 5 times in 100 if you said there was a real difference between the groups involved. Other values showing a progressively better result include p<0.01 (1 in 100), and p<0.001 (1 in a 1000). |
| NS | Non-significant | This abbreviation suggests that there was not a statistical difference between the outcomes of an experimental and control group. Testing has failed to reach the level p<0.05; therefore the study has failed to demonstrate a real difference between the groups concerned. |
| rs | The symbol for Spearman’s rho (pronounced ‘row’) | Used to indicate a correlation between two variables measured at least at ordinal level. The strength of this will be somewhere between +1 and −1. |
| r | The symbol for the Pearson Product-moment (usually referred to as Pearson r) | The same as the above only this is used where both variables are measured at either interval or ratio level. This falls into the category of parametric statistics as it indicates features (parameters) of the population from which the sample is taken. |
| t | The t-test symbol | This parametric test examines the difference in the means of two groups to see if they are statistically different. There are two versions, the t-test for independent samples, i.e. two different groups, and the t-test for matched or paired groups, i.e. the same group before and after an intervention. |
| CI | Confidence Interval | This is an upper and lower figure between which the value measured in the sample is estimated to lie in the population as a whole. |
Finally, at the start of this chapter we should dismiss a common misconception about statistics. It is not true to say ‘you can prove anything with statistics’ – rather, some people can misuse them or ignore the rules that affect their use. This is where the reader must have some understanding of statistics in order to suspect that the results do not support the conclusions being made. However, most research papers are based on a relatively small number of accepted procedures and assumptions. You do not have to understand exactly how something was calculated, as long as you understand the basic principles underpinning its use and you can ‘read’ the symbols and statements used by the researcher.
A simple difference
There are two major categories of statistic used in research: descriptive statistics and inferential statistics. Descriptive statistics use numbers to paint a picture of features or variables found in a sample, whilst inferential statistics are used to apply the findings from the sample to the wider population from which it was taken, or to test the truth of a hypothesis. Inferential statistics are an essential part of RCTs as they indicate the extent to which the intervention introduced by the researcher had an impact on the outcome. Inferential statistics also include the use of correlation; this indicates a pattern or association between variables, for example, in a survey. Each of these two categories of statistic will now be examined.
Descriptive statistics
Quantitative research is concerned with measuring a variable in a way that produces a numeric value. Some variables such as weight, time, and amount of fluid lost have clear operational definitions in the form of standard units of measurement, such as kilograms, minutes and millilitres. For some attributes, such as the physical condition of a baby at birth, scales have been devised in the form of an Apgar score. Other elements such as satisfaction with the birth, or the amount of information received on screening procedures, may have to be turned into numeric values. This is achieved using approximate measures such as Likert scales, where individuals answer a number of statements using options such as ‘strongly agree’, ‘agree’. The researcher then gives each choice a number, such as:
| Strongly agree | Agree | Undecided | Disagree | Strongly disagree |
| 5 | 4 | 3 | 2 | 1 |
The basic principle behind all these procedures is to provide the researcher with some form of numeric measurement that can be processed statistically.
From these examples, it can be seen that some numbers express quantities that are more precise and exact, while others are a more general statement of quantity. Time and volume can be checked and agreed objectively as accurate. Other measurements are less precise and objective, for example, an estimation of blood loss or dilatation of the cervix. This is an important observation, as some researchers will claim a greater degree of objectivity and accuracy for their data than is possible. For some studies, numbers have been produced more as a convenience to allow statistical procedures to take place than as a precise measurement.
Levels of measurement
All numbers look the same. It is possible to construct any combination of numbers you like using the numbers 0 to 9. In statistical theory, numbers are used to represent different ideas, depending on the characteristics of the number. One simple but very important categorisation is the following four levels of measurement:
1. Nominal level (or categorical level)
This is the most basic level. It places or ‘nominates’ a variable into a particular category that is mutually exclusive (it can only be put into one category) and uses a number as a label for that category. So midwives working only in the community may be categorised under the heading ‘1’, and midwives working only in the hospital setting could be categorised as ‘2’, those working in both might be ‘3’. This means that those in the category ‘1’ are the same or equivalent; it does not mean that it takes two community midwives to make one hospital midwife; it just provides a label that happens to be a number, it is not a measurement of quantity. They could just as easily have been labelled using a letter of the alphabet, as in the case of blood groups, a colour or anything else.
2. Ordinal level
As we go up each level, the higher category has the characteristics of the level below, but has extra, more advanced, qualities. So, numbers in this second group not only label a category but also indicate sequence or rank order. For example, arrivals at a clinical area might be given the sequential numeric values 1, 2, 3, 4 to indicate the order in which they entered that area. This would indicate that number 3 was two behind number 1, and one ahead of number 4. However, we cannot do much more with the numbers. We do not know how much later each person was behind the one in front. There may have been a split second between numbers 1 and 2 and several hours before number 3 entered and a day before number 4 entered.
The relevance of this category of measurement is that it takes the same form of the numbers used in a Likert scale or Apgar score. Although the parts of the scale can be labelled 1 to 5, as in the case of a Likert scale, there is no indication of the precise distance between each point. The distance between ‘agree’ and ‘strongly agree’, may not be the same as that between ‘disagree’ and ‘strongly disagree’. All that we can say is that the numbers indicate sequence or rank order along a continuum.
Both nominal and ordinal levels of measurement form a single subcategory in the levels of measurement called categorical data – they put things in categories that are identified by a number, and do not measured quantitatively. They both possess very basic properties that restrict the statistical procedures that can be carried out on them. The next two categories are far more sophisticated and provide more useful information.
3. Interval level
This level produces numbers that allocate units to a category, indicate sequence, but this time the distances between the different points are the same. This means that they can be ‘averaged’, and have other procedures carried out on them. Along with the next category, the interval level indicates ‘true numbers’ that measures amounts, and does not simply use numbers as a label.
4. Ratio level
This is the final, and highest, level of measurement. It is very much like the interval level except for one crucial factor, and that is there is an absolute zero point in the measurement scale below which it is impossible to record a value. For example, temperature readings in Fahrenheit or centigrade are interval level because it is possible to have a minus figure, such as minus five degrees centigrade. This is because zero in Fahrenheit and centigrade are arbitrary points, not an absolute zero. Height, age and weight are all ratio level as it is impossible to have less than a zero amount of any of them.
The importance of the last two levels of measurement is that they quantify something, and they are always measured in units of some kind, such as kilograms, hours and minutes, centilitres. It is this property that makes them suitable for statistical procedures in that the other levels of nominal and ordinal do not measure the quantity of anything but simply categorise, using numbers to label the categories, and in the case of ordinal data, place them in sequence. For this reason, the interval and ratio levels are classed as numeric levels and the nominal and ordinal levels are seen as categorical levels. The key characteristics of these four levels of measurement are summarised in Table 13.2.
| Level | Properties | Characteristics |
|---|---|---|
| Nominal | Most basic of all | Names, categorises variables |
| Ordinal | Basic non-measurement | Numbers used to categorise into sequence or ‘rank order’ |
| Interval | Measures properties of variable | Equal distance between units; no absolute zero. Sophisticated statistical procedures possible |
| Ratio | Highest level | Absolute zero, equal distance between units. Suited to sophisticated statistical procedures |
Space has been devoted to the explanation of these levels as many of the principles of statistical analysis are based on this categorisation system; therefore, their importance to understanding statistics should not be underestimated. In the next section we turn to the problem of making descriptive statistics meaningful to the reader.
Summarising descriptive data: measures of central tendency
Burns and Grove (2009) point out that although analysing the results of a study is one of the most exciting parts of a study for the researcher, this can be one of the most challenging aspects for the reader of a research report. Yet the reason for processing data is to make them easier to understand. It is no use presenting results in terms of each person’s answers to a questionnaire or physical assessment expressed in the numeric values for each answer, as in the following:
| Respondent A: | 21 | 2 | 29 | 17 | 2 | 55 | 34 | 23 | 7 | 81 | 64 | 34 | 3 | 29 | 46 | 50 |
| Respondent B: | 18 | 37 | 4 | 21 | 31 | 8 | 30 | 15 | 1 | 2 | 57 | 41 | 75 | 4 | 7 | 47 |
It would mean very little as it is not clear to what the numbers relate, and there is no pattern visible that makes sense between the two respondents. The answer is to use summary statistics that allow us to convey meaning by summarising quite large collections of numbers.
The most successful form of summary statistic is the measure of central tendency. This is a clumsy way of saying the number that appears typical in the group, or the number that represents the central value found in the entire collection of results (data set). If you are thinking ‘that sounds like the average’ you would be right, but in statistics there are a number of different ways of calculating ‘the average’, each known by a different name.
1. Mean
This is what we commonly call the ‘average’. For instance, we might say ‘on average, I take half an hour to get home from work’, or we might read that ‘on average, people watch television for four hours a day’. We don’t mean that the figure is exact; sometimes it may be more, sometimes in may be less, but when we even things out it is reasonably typical.
It is not difficult to calculate the ‘average’ or ‘mean’ of something. If you had to work out the average length of time that 10 members of staff in your clinical area had been qualified, you would ask each one how long they had been qualified, add them all together and divide by the total number of people. Easy! To write down that process so others could repeat it, the statistician would symbolise each stage to produce the following formula:
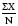
The symbols translate as:
Σ = Add together each of the following
X = The numeric value of the item you are interested in from each person
— = The sign for ‘divide by’ used in a fraction
N = The total number in the group.
The formula looks baffling, but understanding the symbols, and the sequence in which to carry out the procedures, makes it clearer. This is how even the most complicated formulae work; each symbol is translated into an instruction that is carried out in a set sequence.
The mean can only be calculated if the level of data is either interval or ratio, that is, where the numbers reach a numeric level of measurement and are actually measuring something in recognisable units of quantity. It does not work for categorical data such as calculating the average star sign of people in a group where Aquarius = 1, Pisces = 2, etc. Neither does it really work with ordinal data, although you will see an average figure for Likert scale values calculated.
There is one big drawback in using the mean, and that is it is influenced by untypical numbers that are much higher or much lower than the majority of other numbers in the group or ‘data set’. These more extreme values are called ‘outliers’, because when individual results are plotted on a graph, they are the ones that stand out because they are out of line with the main results. The result would be an untypical value of what is typical in the group and so we can sometimes be misled by the mean for a group of results because there may be a small number of untypical results pulling the mean up or down. This is illustrated in Box 13.1.
BOX 13.1
Ages of those attending a restaurant party
a) Ages of a group of children going to a birthday party
6 6 8 8 9 9 10 11 11
median = 9, mean = 8.6
b) Ages of children plus Grandma and her twin sister Elsie going to a birthday party
6 6 8 8 9 9 10 72 72
median = 9, mean = 22.2
Punch line: The median is a more stable calculation, as outliers (untypical large or small figures) do not influence it; the mean is influenced by outliers and can produce an unrepresentative figure.
2. Median
The median is a useful calculation of central tendency, as it is not influenced by extreme values. The median is calculated by taking every single figure in the set of numbers, such as length of second stage of labour for 20 women. They are all then put in rank order from the smallest to the biggest. The median is the value of the unit in the middle of this row or distribution of numbers.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


Get Clinical Tree app for offline access
