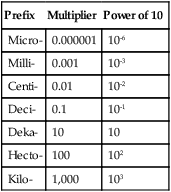
Upon completion of this chapter, the learner will be able to: 1. Define the key terms that relate to the chapter. 2. Describe movement of the decimal when working with the metric system. 3. Calculate metric conversions using the power of 10. 4. Define significant figures. 5. Rewrite problems using standard scientific notation. 6. Use a calculator to solve problems written in standard scientific notation. Many students find larger numbers or numbers with decimals intimidating. As we have discussed, the larger the number, the greater the chance of error—and errors can affect a patient’s rate of recovery. In this chapter, we discuss strategies for reducing large numbers by using the principles of power of 10 or writing numbers in scientific notation. Exponents are used to represent large base 10 numbers and when writing numbers in scientific notation. If you are unsure of how to manipulate exponents or negative numbers, you might want to review the relevant sections in Chapter 1. In Chapter 7, you learned the prefixes that are used in the metric system. Because the metric system is based on the power of 10, it is common to solve the conversion problems using mental math or manipulation of the decimal point. Table 10-1 demonstrates the power of 10 written as an exponent and as the multiplier. Table 10-1 Metrix Prefixes as Power of 10 100 × 1,000 10,000 ÷ 100 Chapter 5 discussed the way to set up proportions and ratios so that you could convert between metric measurements to find the equivalent value. Since the metric system is based on the power of 10, many students find it easier to convert similar measurements by manipulating the decimal point rather than setting up the problem as a proportion. When the conversion is from a larger to a smaller metric unit, the decimal point moves to the right. When a smaller metric unit is being converted to a larger one, the decimal point moves to the left (Table 10-2). Table 10-2 How many micrograms are in 0.5 mg>?
Power of 10
Objective 1
Objective 2
Power of 10
Prefix
Multiplier
Power of 10
Micro-
0.000001
10-6
Milli-
0.001
10-3
Centi-
0.01
10-2
Deci-
0.1
10-1
Deka-
10
10
Hecto-
100
102
Kilo-
1,000
103
Objective 3
Multiplication and division by the power of 10
Example:
Example:

Example:
14.118 × 100

Example:
310199.1 ÷ 10,000
The correct answer is 31.01991.

Conversion Between Metric Units
Direction of Movement in Problem
Movement of Decimal
Multiply by Multiplier?
Divide by Multiplier?
From a larger metric unit to a smaller metric unit
Right
Yes
No
From a smaller metric unit to a larger metric unit
Left
No
Yes

Example:

Objective 4
Significant figures
Example:
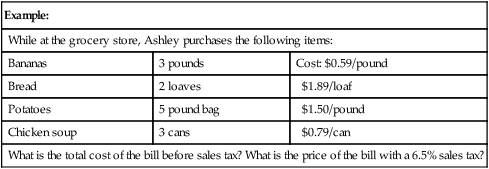
While at the grocery store, Ashley purchases the following items:
Bananas
3 pounds
Cost: $0.59/pound
Bread
2 loaves
$1.89/loaf
Potatoes
5 pound bag
$1.50/pound
Chicken soup
3 cans
$0.79/can
What is the total cost of the bill before sales tax? What is the price of the bill with a 6.5% sales tax?

 PRACTICE THE SKILL 10-1
PRACTICE THE SKILL 10-1 MATH ETIQUETTE 10-1
MATH ETIQUETTE 10-1 PRACTICE THE SKILL 10-2
PRACTICE THE SKILL 10-2 STRATEGY 10-1
STRATEGY 10-1
 STRATEGY 10-2
STRATEGY 10-2
 PRACTICE THE SKILL 10-3
PRACTICE THE SKILL 10-3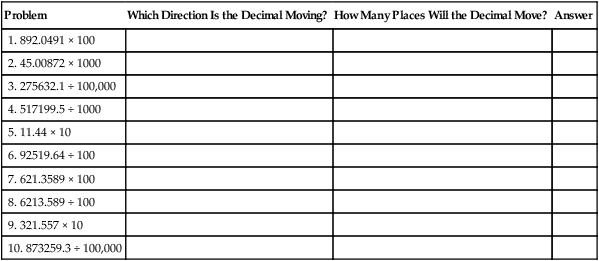
 MATH IN THE REAL WORLD 10-1
MATH IN THE REAL WORLD 10-1
 BUILDING CONFIDENCE WITH THE SKILL 10-1
BUILDING CONFIDENCE WITH THE SKILL 10-1 MATH ETIQUETTE 10-2
MATH ETIQUETTE 10-2

