Organization and presentation of data

15


Organization and presentation of data




Introduction


The summary and interpretation of data from quantitative research entail the use of statistics. A statistic is a number that is obtained by the mathematical manipulation of the data. We use descriptive statistics to describe data and inferential statistics to analyse research observations and measurements.


In previous chapters we examined how interviews, observations and measurement are used to produce data in clinical investigations or research. It can be difficult to make sense of raw data when they consist of a large number of measurements. Before we can interpret or communicate the information provided by a research project, the raw data must be organized and presented in a clear and intelligible fashion. We do this using descriptive statistics. 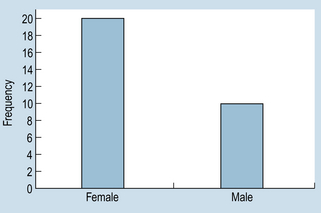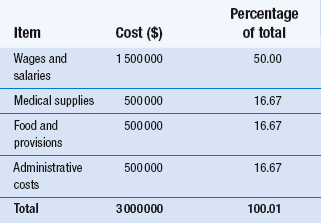In this chapter we will outline methods used in descriptive statistics for the organization, tabulation and graphic presentation of data. We will also examine the use of some simple statistics directly derived from the tabulation of the data.


The aims of this chapter are to:




The organization and presentation of nominal or ordinal data


A primary consideration in selecting appropriate statistics is the question of whether the data are discrete or continuous. Scaled data are necessarily discrete, so that the organization of the data involves counting the number (frequency) of cases falling into each category of measurement. Let us examine two hypothetical examples as an illustration.



Organization of discrete data



Example 1: nominal (categorical) data


We are interested in the sex of patients (these are nominal or categorical data) undergoing gall bladder surgery (cholecystectomy) at a public hospital over a period of one year. The raw data indicating the sex (M or F) of the patients is simply read off the patients’ records, as follows:



Grouping the above nominal data involves counting the number of cases (or measurements) falling into each category. The total is M = 10 and F = 20. The data can be presented in tabular form. Table 15.1 shows the following conventions in tabulating data:





Example 2: ordinal data


Ordinal data are presented by counting the number of cases (frequency) of each ordered rank making up the scale.


An investigator intends to evaluate the effectiveness of a new analgesic versus placebo treatment. A post-test only control group design is used: the experimental group receives the analgesic and the control group receives the placebo. Twenty patients are randomly assigned into each of the two groups. Pain intensity is assessed by the patients’ pain reports five hours after minor surgery, on the following scale:



The raw data are:



After tallying the results, the above data can be presented as a frequency distribution, as shown in Table 15.2. This demonstrates that, when the data have been tabulated, we can see the outcome of the investigation. Here, the pain reported by the experimental group is less than that of the control group. Organizing the data is the first step in producing evidence for testing the hypothesis that the new analgesic is more effective than placebo.




Graphing discrete data


Once a frequency distribution of the raw data has been tabulated, a variety of techniques is available for the graphical presentation of a given set of measurements. Frequency distributions of qualitative data are often plotted as bar graphs (also termed ‘column’ graphs), or shown pictorially as pie diagrams.


A bar graph involves plotting the frequency of each category and drawing a bar, the height of which represents the frequency of a given category. Figure 15.1 graphs the data given in Table 15.1.



Figure 15.1 demonstrates conventions in plotting bar graphs:



It should be noted that care must be exercised in interpreting graphs, as the axes may be translated or compressed causing a false visual impression of the data. Make sure that you inspect the values along the axes, so that you are not misled. It is also acceptable to calculate the percentage of scores falling into each category and to display the percentages instead of frequencies.


It can be seen in Figure 15.2 that, by presenting the data for the experimental and control groups on the same graph, the reader gains a visual impression of the possible effectiveness of the analgesic treatment in contrast to that of the control intervention or treatment. Nominal data can also be meaningfully presented as a pie chart, where the percentage of each category is converted into a proportional part of a circle or ‘pie’. For example, in a given hospital we have the hypothetical spending patterns shown in Table 15.3.


Related posts:

  1. Surveys and quasi-experimental designs
  2. 11:Questionnaires
  3. Effect size and the interpretation of evidence
  4. Standard scores and normal distributions

Stay updated, free articles. Join our Telegram channel
Tags:
Apr 12, 2017 | Posted by in MEDICAL ASSISSTANT | Comments Off on Organization and presentation of data

Full access? Get Clinical Tree
Get Clinical Tree app for offline access