DEDUCTION

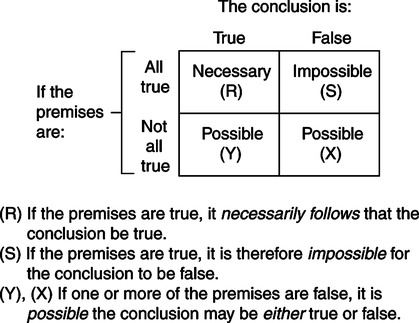
Deduction is the form in which specific conclusions are inferred from more general premises or assertions. Reasoning proceeds from general assertions to specific conclusions. A theory that is developed deductively follows a process with a sequence of premises called axioms, that is, statements or propositions that derive from broader premises. The concluding statement is an unknown that leads to theoretical prediction and formation of hypotheses to be tested empirically. A very basic deductive example is as follows:

In logical analysis, letters may be substituted for concepts to keep the emphasis of the analysis focused on the form of argument. The examples below illustrate the process of deductive reasoning.

In Examples A and B, the conclusions follow or are deduced from general premises of what is known. Deductive reasoning is based on what is known, and the conclusion represents something yet to be verified in clinical research. Only information presented in the premises is presented in the conclusion. Usually, a number of premises in a proposal lead to the conclusion.

In the nursing literature, you may find the deductive form, whereby authors present their logic for deriving a theory from a nursing model (particularly a middle range theory). This process of premises and conclusions, performed in sequence and clearly labeled, is included more often in dissertations. Once deductive reasoning is learned, it is possible to identify and label the premises and conclusions when reading narrative text (Salmon, 1973). Salmon suggests certain words or phrases as clues that indicate specific statements presented as premises or conclusions. Terms that often precede a premise are connecting words such as since, for, and because. Terms that often precede a conclusion are therefore, consequently, hence, so, and it follows that (Salmon, 1973).

A nursing theory example developed through the use of deductive logic is the Roy Adaptation Model. Roy used Helson’s (1964) adaptation-level theory as the general premise for her nursing model. Helson presented the behavioral response (of the eye) to stimuli in modes of adaptation to changes in the environment. He labeled stimuli with three classes of cues: focal, contextual, and organic. Working from Helson’s premises about adaptation, Roy developed the premise for her theory of the person as an adaptive system and her adaptation model. Tsai (2003) utilized the Roy Adaptation Model to develop a middle range theory of caregiver stress by selecting concepts and specifying their relationships in the context of caregivers and the chronically ill (a full discussion of Roy’s theoretical work can be found in Chapter 17 of this text). Example C displays deductive reasoning as used in the Roy Adaptation Theory.

The argument may be evaluated in at least two different ways as follows: (1) The validity of the conclusion may be assessed as to whether it logically follows the premises, and (2) the content of the premises may be assessed in terms of the truth or falsity of the statements (Pospesel, 1974). So if you look at example C, the argument can be evaluated by asking these questions: Are the premises true statements? Is the conclusion valid? Do the premises support the conclusion?

The validity of a deductive argument refers to the logic involved in reasoning from the premises to the conclusion, to ensure that, if the premises are true, the conclusion must be true (Pospesel, 1974; Salmon, 1973; Steiner, 1978). A deductive argument may contain all true statements, or one or more false statements, and it may be considered valid or invalid. This judgment is made on the basis of whether the conclusion is supported by the premises.

Although Justin may be the victim of abuse, the truth or falsity of the conclusion or of any of the statements is not an issue when the validity of an argument is evaluated. In Example D, the premises do not present any supportive evidence that Justin is a victim of abuse. Further, the premises do not assert that only victims of abuse have low self-esteem. Justin’s low self-esteem could be the result of other antecedents or causes, such as he may have significant physical deformities and poor social support that negatively influenced his social development. The conclusion therefore goes beyond the explicit and implicit information in the premises. This is not a valid argument. Compare the reasoning in Examples A and B and C with that in Example D. Validity refers to the form of the deductive argument, and truth refers to the content of a given theoretical statement. Therefore, it is inappropriate to label a single theoretical statement as valid or to label an argument as true (Salmon, 1973).

In a valid deductive argument, if the premises are true, the conclusion must be true. This combination is marked (R) in Figure 3-1. It is impossible for the conclusion to be false. This combination is marked (S) in Figure 3-1. However, if one or more of the premises is false, two outcomes are possible: The conclusion may be either true or false.

Example E presents a deductively valid argument that illustrates how false premises may lead to a false conclusion. This combination is marked (X) in Figure 3-1.

As Figure 3-1 suggests and as Example E illustrates, it is possible that a valid argument can lead to one or more false premises and a true conclusion. This combination is marked (Y) in Figure 3-1.

It may be helpful to study Examples E and F to understand how conclusions derive from the information given in the premises. In science, deductive arguments are a powerful form of reasoning to derive new conclusions in that they explicate implied information. The derived conclusion then is subjected to hypotheses and empirical testing to determine whether what was logically concluded corresponds with research findings.

The use of deductive reasoning in a clinical discipline such as nursing requires one to move from the de-contextualized world (an isolated laboratory) to a real life situation (a clinical setting), where one is influenced by emotional and social factors (Smorti, 2008). Human science is an inexact science for this very reason, and the possibility of invalid deductive logic exists. For example, if one believes as a true statement that every patient with hypothyroidism has an abnormal TSH (thyroid-stimulating hormone) test, how does one explain a patient with a normal TSH with hypothyroidism? Use of a universal law to explain patient situations is flawed. Elements of uncertainty in all healthcare decisions require providers to use probability and other forms of reasoning such as inductive reasoning (Soltani & Moayyeri, 2007).

INDUCTION

Induction is a form of logical reasoning in which a generalization is induced from a number of specific, observed instances. Inductive reasoning is not as clearly developed as deductive reasoning (Pospesel, 1974). The form of the inductive argument is as follows:

The inductive form is based on the assumption that members of any given class share common characteristics. Therefore, what is true for any randomly selected member of the class is accepted as true for all members of the class (Steiner, 1978). Suppose a sample of abuse victims has been selected for study. Example G presents an argument in the inductive form that may be developed on the basis of this hypothetical study.

In another study, a sample of the population of fathers and their newborns has been selected for study. Fathers selected for the study live in the southern city of Charlotte, North Carolina, and are white collar professionals and Asian. Example H presents an argument in the inductive form that may be developed on the basis of a father-newborn pair study of bonding.

The premise in Example H states observations from a number of instances, that is, a limited number of subjects and limited to one ethnic, regional, and socioeconomic group. The conclusion states a generalization that extends beyond these observations to the entire class of fathers and their newborns.

The inductive generalization may be stated in terms of a mathematical quantity (Salmon, 1973). For example, assume a researcher surveys a sample of 400 nurses to learn their opinions about whether nurses should establish independent private practices. Results indicate that 60% of those nurses support independent private practice activities in nursing. The inductive statement may be stated as follows.

Stay updated, free articles. Join our Telegram channel

Join