20 Hypothesis testing is the process of deciding using statistics whether the findings of an investigation reflect chance or real effects at a given level of probability or certainty. If the results seem to not represent chance effects, then we say that the results are statistically significant. That is, when we say that our results are statistically significant we mean that the patterns or differences seen in the sample data are likely to be generalizable to the wider population from our study sample. The following steps are conventionally followed in hypothesis testing: 1. State the alternative hypothesis (HA), which is the based on the research hypothesis. The HA asserts that the results are ‘real’ or ‘significant’, i.e. that the independent variable influenced the dependent variable, or that there is a real difference among groups. The important point here is that HA is a statement concerning the population. A real or significant effect means that the results in the sample data can be generalized to the population. 2. State the null hypothesis (H0), which is the logical opposite of the HA. The H0 claims that any differences in the data were just due to chance: that the independent variable had no effect on the dependent variable, or that any difference among groups is due to random effects. In other words, if the H0 is retained, differences or patterns seen in the sample data should not be generalized to the population. 3. Set the decision level, α (alpha). There are two mutually exclusive hypotheses (HA and H0) competing to explain the results of an investigation. Hypothesis testing, or statistical decision making, involves establishing the probability of H0 being true. If this probability is very small, we are in a position to reject the H0. You might ask ‘How small should the probability (α) be for rejecting H0?’ By convention, we use the probability of α = 0.05. If the H0 being true is less than 0.05, we can reject H0. We can choose an α of 0.05, but not more, That is, by convention among researchers, results are not characterized as significant if p > 0.05. 4. Calculate the probability of H0 being true. That is, we assume that H0 is true and calculate the probability of the outcome of the investigation being due to chance alone, i.e. due to random effects. We must use an appropriate sampling distribution for this calculation. 5. Make a decision concerning H0. The following decision rule is used. If the probability of H0 being true is less than α, then we reject H0 at the level of significance set by α. However, if the probability of H0 is greater than α, then we must retain H0. In other words, if: 1. We can state two competing hypotheses concerning the outcome of the game: a. the authors fixed the game; that is, the outcome did not reflect the fair throwing of a coin. Let us call this statement the ‘alternative hypothesis’, HA. In effect, the HA claims that the sample of 10 heads came from a population other than P (probability of heads) = Q (probability of tails) = 0.5 b. the authors did not fix the game; that is, the outcome is due to the tossing of a fair coin. Let us call this statement the ‘null hypothesis’, or H0. H0 suggests that the sample of 10 heads was a random sample from a population where P = Q = 0.5. 2. It can be shown that the probability of tossing 10 consecutive heads with a fair coin is actually p = 0.001, as discussed previously (see Ch. 19). That is, the probability of obtaining such a sample from a population where P = Q = 0.5 is extremely low. 3. Now we can decide between H0 and HA. It was shown that the probability of H0 being true was p = 0.001 (1 in a 1000). Therefore, in the balance of probabilities, we can reject it as being true and accept HA, which is the logical alternative. In other words, it is likely that the game was fixed and no ≤10 cheque needed to be posted. The probability of calculating the truth of H0 depended on the number of tosses (n = the sample size). For instance, the probability of obtaining heads every times with five coin tosses is shown in Table 19.4. As the sample size (n) becomes larger, the probability for which it is possible to reject H0 becomes smaller. With only a few tosses we really cannot be sure if the game is fixed or not: without sufficient information it becomes hard to reject H0 at a reasonable level of probability. 1. State HA: ‘The exercise program reduces the time taken for patients to recover from orthopaedic surgery’. That is, the researcher claims that the independent variable (the treatment) has a ‘real’ or ‘generalizable’ effect on the dependent variable (time to recover). 2. State H0: ‘The exercise program does not reduce the time taken for patients to recover from orthopaedic surgery’. That is, the statement claims that the independent variable has no effect on the dependent variable. The statement implies that the treated sample with 3. The decision level, α, is set before the results are analysed. The probability of α depends on how certain the investigator wants to be that the results show real differences. If he set α = 0.01, then the probability of falsely rejecting a true H0 is less than or equal to 0.01 (1/100). If he set α = 0.05, then the probability of falsely rejecting a true H0 is less than or equal to 0.05 or (1/20). That is, the smaller the α, the more confident the researcher is that the results support the alternative hypothesis. We also call α the level of significance. The smaller the α, the more significant the findings for a study, if we can reject H0. In this case, say that the researcher sets α = 0.01. (Note: by convention, α should not be greater than 0.05.) 4. Calculate the probability of H0 being true. As stated above, H0 implies that the sample with Figure 20.1 Sampling distribution of means. Sample size = 64, population mean = 30, standard deviation = 8. 5. Make a decision. We have set α = 0.01. The calculated probability was less than 0.0001. Clearly, the calculated probability is far less than α, indicating that the difference is unlikely to be due to chance. Therefore, the investigator can reject the statement that H0 is true and accept HA, that patients in general treated with the exercise program recover earlier than the population of untreated patients. In Section 5 we saw that the selection of appropriate descriptive statistics depends on the type of data being described. For example, in a variable such as incomes of patients, the best statistics to represent the typical income would be the mean and/or the median. If you had a millionaire in the group of patients, the mean statistic might give a distorted impression of the central tendency. In this situation the median statistic would be the most appropriate one to use. The mode is most commonly used when the data being described are categorical data. For example, if in a questionnaire respondents were asked to indicate their sex and 65% said they were male and 35% said they were female, then ‘male’ is the modal response. It is quite unusual to use the mode only with data that are not nominal. As a rule, the scale of measurement used to obtain the data and its distribution determine which descriptive statistics are selected. In the same way, the appropriate inferential statistics are determined by the characteristics of the data being analysed. For example, where the mean is the appropriate descriptive statistic, the inferential statistics will determine if the differences between the means are statistically significant. In the case of ordinal data, the appropriate inferential statistics will make it possible to decide if either the medians or the rank orders are significantly different. With nominal data, the appropriate inferential statistic will decide if proportions of cases falling into specific categories are significantly different.
Hypothesis testing
selection and use of statistical tests
The logic of hypothesis testing
Steps in hypothesis testing
Illustrations of hypothesis testing
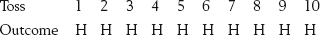
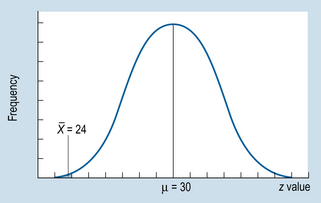
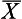 = 24, and n = 64 is in fact a random sample from the population µ = 30, σ = 8. Any difference between
= 24, and n = 64 is in fact a random sample from the population µ = 30, σ = 8. Any difference between 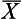 and µ can be attributed to sampling error.
and µ can be attributed to sampling error.
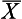 = 24 is a random sample from the population with µ = 30, σ = 8. How probable is it that this statement is true? To calculate this probability, we must generate an appropriate sampling distribution. As we have seen in Chapter 17, the sampling distribution of the mean will enable us to calculate the probability of obtaining a sample mean of
= 24 is a random sample from the population with µ = 30, σ = 8. How probable is it that this statement is true? To calculate this probability, we must generate an appropriate sampling distribution. As we have seen in Chapter 17, the sampling distribution of the mean will enable us to calculate the probability of obtaining a sample mean of 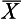 = 24 or more extreme from a population with known parameters. As shown in Figure 20.1, we can calculate the probability of drawing a sample mean of
= 24 or more extreme from a population with known parameters. As shown in Figure 20.1, we can calculate the probability of drawing a sample mean of 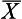 = 24 or less. Using the table of normal curves (Appendix A), as outlined previously, we find that the probability of randomly selecting a sample mean of
= 24 or less. Using the table of normal curves (Appendix A), as outlined previously, we find that the probability of randomly selecting a sample mean of 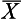 = 24 (or less) is extremely small. In terms of our table, which only shows the exact probability of up to z = 4.00, we can see that the present probability is less than 0.00003. Therefore, the probability that H0 is true is less than 0.00003.
= 24 (or less) is extremely small. In terms of our table, which only shows the exact probability of up to z = 4.00, we can see that the present probability is less than 0.00003. Therefore, the probability that H0 is true is less than 0.00003.
The relationship between descriptive and inferential statistics
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


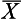 = 24 days. Do these results show that patients who had the treatment recovered significantly faster than previous patients? We can apply the steps for hypothesis testing to make our decision.
= 24 days. Do these results show that patients who had the treatment recovered significantly faster than previous patients? We can apply the steps for hypothesis testing to make our decision.