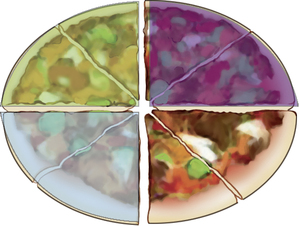
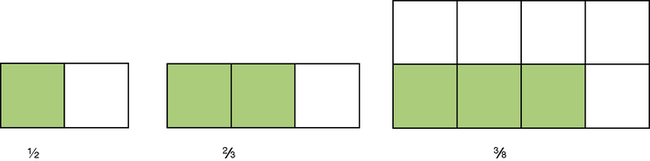
Upon completion of this chapter, the learner will be able to: 1. Define the key terms that relate to fractions. 2. Identify situations in health care professions that benefit from use of fractions. 3. Manipulate fractions into a specified order of value with 100% accuracy. 4. Manipulate fractions from an improper fraction to a mixed number and from a mixed number to an improper fraction with 100% accuracy. 5. Perform the following mathematical operations involving fractions with 100% accuracy: addition, subtraction, multiplication, and division. A number that is a factor of two or more numbers. The number of equal parts in a whole. It is the bottom number of a fraction. Fractions that represent the same relationship of part to the whole. The fractions are equal even though there are variations in the size of the pieces or the number of parts of the total. The number being multiplied. A ratio that represents part of something in comparison to the total number of parts. Fractions with Common Denominators Fractions that have the same denominator. The largest factor of two or more numbers. A fraction in which the numerator is greater than the denominator. Least Common Denominator (LCD) The smallest common multiple of the denominators of two or more fractions. A number expression that consists of a whole number and a fraction. The number of parts to which the problem is referring. It is the top number of a fraction. A fraction in which the denominator is greater than the numerator. Finding the lowest equivalent fraction by dividing the numerator into the denominator. This is done by finding the greatest common factor of the numerator and the denominator. Part of a mixed number that is not in fractional form. • Medical assistant: preparing medications, measuring height and weight, measuring for the length of a cast or splint • Pharmacy technician: assisting in the preparation of medication • Physical therapy assistant: supervising rehabilitation exercises involving weights, documenting endurance in minutes or hours • Nurse: administering medication, IV therapy, and blood transfusions • Dietician: calculating dietary intake or calorie needs • Paramedic: preparing medication doses based on weight, calculating length of time for transport from a scene Example: Three friends have ordered a pizza. The pizza comes in eight slices. Each friend has two slices (Figure 3-1). Describe what fraction of the pizza has been eaten: 3 friends × 2 slices each = 6 slices of pizza eaten. The pizza had a total of 8 slices. What is the fractional expression for the amount of pizza that has not been consumed? 8 total slices – 6 slices already eaten = 2 slices left. So, the fraction of the pizza has not been consumed is As we have learned, fractions are a descriptive way to identify a portion, either used or remaining, of the total. For the visual learners and kinesthetic learners of the world, however, fractions can be hard to visualize. If you are having problems in determining the size of a series of fractions, try drawing a box into the number of sections indicated in the denominator and then shading the sections indicated in the numerator (Figure 3-2).
Fractions
Objective 1
Objective 1
What Is a Fraction?
Example: Figure of a fraction: 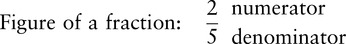
Many people learned fractions by visualizing a pizza pie. So, let’s take what we know and apply it.

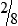 , or
, or 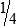 .
.
Objective 2
Why Do We Use Fractions?
Objective 4
Different Types of Fractions
Example:
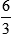
6 divided by 3 = 2
Most improper fractions will not divide evenly to create a whole number. Most improper fractions will have a whole number and a fraction.

Example:
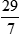
29 divided by 7 = 4 with a remainder of 1; the remainder is placed in the numerator and the denominator remains unchanged, so the answer is written as 4 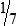 .
.

Example:
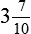
Multiply the denominator by the whole number: 10 × 3 = 30.
Then add the numerator: 30 + 7 = 37.
The number 37 is your new numerator and will go over the existing denominator.
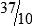 is your improper fraction.
is your improper fraction.

Objective 5
Addition and subtraction of fractions
Ryan’s time sheet for work:
Monday
6 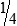 hours
hours
Thursday
4 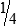 hours
hours
Saturday
5 hours

6 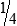
Add the numerators.
4 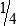
The denominators will remain the same, since they are common.
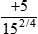
Add the whole numbers.

Fractions
Get Clinical Tree app for offline access

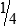
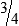
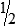
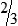
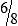
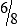
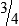
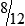
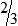
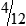
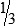
 STRATEGY 3-1
STRATEGY 3-1 PRACTICE THE SKILL 3-1
PRACTICE THE SKILL 3-1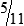
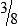
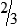
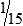
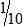
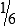
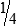
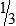
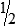
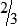
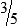
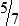
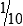
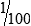
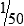
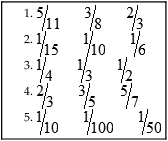
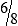
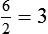
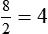
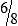
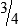
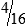
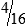
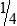
 HUMAN ERROR 3-1
HUMAN ERROR 3-1 BUILDING CONFIDENCE WITH THE SKILL 3-1
BUILDING CONFIDENCE WITH THE SKILL 3-1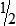
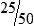
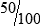
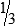
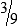
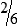
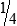
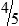
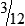
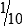
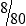
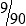
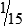
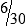
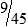
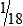
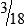
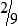
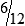
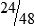
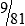
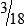
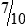
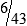
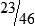
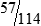
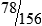
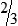
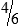
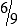
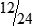
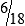
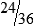
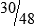
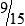
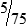
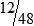
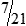
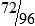
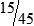
 MATH ETIQUETTE 3-1
MATH ETIQUETTE 3-1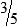
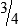
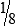
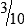
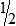
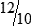
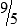
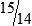
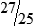
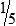
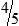
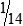
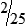
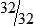
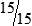
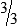
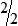
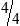
 HUMAN ERROR 3-2
HUMAN ERROR 3-2 MATH ETIQUETTE 3-2
MATH ETIQUETTE 3-2 STRATEGY 3-2
STRATEGY 3-2 STRATEGY 3-3
STRATEGY 3-3 PRACTICE THE SKILL 3-2
PRACTICE THE SKILL 3-2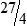
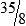
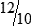
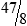
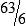
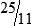
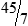
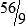
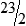
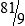
 PRACTICE THE SKILL 3-3
PRACTICE THE SKILL 3-3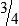
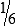
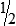
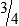
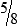
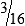
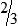
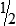
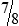
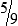
 BUILDING CONFIDENCE WITH THE SKILL 3-2
BUILDING CONFIDENCE WITH THE SKILL 3-2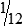
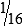
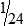
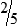
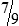
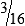
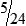
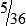
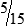
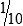
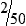
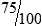
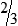
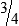
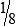
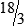
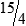
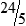
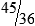
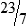
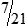
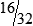
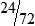
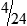
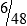
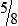
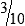
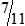
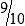
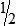
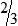
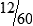
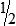
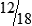
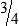
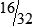
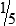
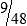
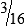
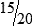
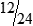
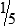
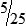
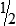
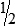
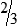
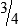
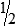
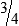
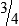
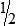
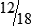
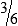
 HUMAN ERROR 3-3
HUMAN ERROR 3-3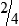
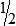
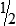
 STRATEGY 3-4
STRATEGY 3-4 PRACTICE THE SKILL 3-4
PRACTICE THE SKILL 3-4











