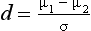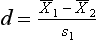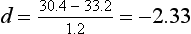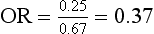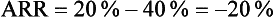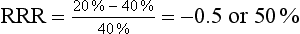Effect size and the interpretation of evidence

Introduction

When researchers have demonstrated statistical significance within the results of a study, what have they actually done? Statistical significance indicates that the results obtained in the study are probably not just due to chance but represent support for the study research hypothesis. However, it is not correct to assume that having established statistical significance means that the results are clinically important or useful for guiding our practices. We must also establish the clinical or practical significance of our results following the step of demonstrating statistical significance.

So how do we do that? The practical significance of the results depends on a statistic referred to as the ‘effect size’; the larger the ‘effect size’, the more likely it is that the results will be clinically useful. As we will see in this chapter, effect size is the most relevant statistic for establishing the efficacy of an intervention.

The aims of this chapter are to discuss the following:

1. Effect size, that is how large the relationships or differences observed in the data are.

2. The relationship between effect size and statistical and clinical significance.

3. The determinants of statistical power.

4. Basic principles of clinical decision making.

Effect size

Effect size expresses the size of the change or degree of association that can be attributed to a health intervention. The term effect size is also used more broadly in statistics to refer to the size of the phenomenon under study. For example, if we were studying gender effects on how long people live, a measure of effect size could be the difference in life expectancy between males and females. On average, this difference is actually around 5 years, which has real implications! In a correlational study, the effect size is the size of the correlation between the selected variables under study (e.g. r² as discussed in Chapter 18). There are many measures or indicators of effect size; the one which is relevant to analysing the results of a study is selected on the basis of the scaling of the outcome or dependent variable (Sackett et al 2000).

Effect size with continuous data

The concept of effect size for continuous data (i.e. an interval or ratio measurement scale) can be illustrated by results from two student research projects supervised by one the authors.

Study 1: Test–retest reliability of a force measurement machine

In this first study, the student was concerned with demonstrating the test–retest reliability of a device designed to measure maximum forces being produced by patients’ leg muscles under two conditions (flexion and extension). Twenty-one patients took part in the study and the reliability of the measurement process was tested by taking two readings for the same patients an hour apart and then calculating the Pearson correlation between the readings obtained from the machine in question during two trials separated by an hour for each patient. The results are shown in Table 21.1. Both results reached the p = 0.01 level of significance.

Table 21.1

Pearson correlations between trials 1 and 2

The student was ecstatic when the computer data analysis program informed that the correlations were statistically significant at the 0.01 level (indicating that there was less than a 1 in 100 chance that the correlations were illusory or actually zero). We were somewhat less ecstatic because, in fact, the results indicated that approximately 69% (1 – 0.56²) and 71% (1 – 0.54²) of the variation was not shared between the measurements of the first and second trial. In other words, the measures were ‘all over the place’, despite statistical significance being reached. Thus, far from being an endorsement of the measurement process, these results were somewhat of a condemnation. This is a classic example of the need for careful interpretation of effect size in conjunction with statistical significance.

Study 2: A comparative study of improvement in two treatment groups

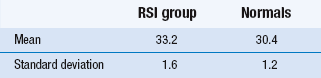
The second project was a comparative study of two groups: one group suffering from suspected repetition strain injuries (RSI) induced by frequent computer data entry and a group of ‘normals’. An activities of daily living (ADL) assessment scale was used and yielded a ‘disability’ index of between 0 and 50. There were 60 people in each group. The results are shown in Table 21.2.

Table 21.2

Mean ADL disability scores

The appropriate statistic for analysing these data happens to be the independent groups t test, although this is not important for understanding this example. The t value for these data was significant at the 0.05 level. Does this finding indicate that the difference is clinically meaningful or significant? There are two steps in interpreting the clinical significance of the results.

First, we calculate the effect size. For interval or ratio-scaled data the effect size ‘d’ is defined as:

where µ₁−µ₂ refers to the difference between the population means and σ refers to the population standard deviation.

Since we rarely have access to population data we use sample statistics for estimating population differences. The formula becomes:

where 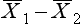indicates the difference between the sample means and s₁ refers to the standard deviation of the ‘normal’ or ‘control’ group. Therefore, for the above example, substituting into the equation yields:

In other words, the average ADL score of the people with suspected RSI was 2.33 standard deviations under the mean of the distribution of ‘normal’ scores. The meaning of d can be interpreted by using standardized scores. The greater the value of d, the greater the standardized difference between the means and therefore the larger the effect size.

Second, we need to consider the clinical implications of the evidence. It might be that the difference of 2.8 units in the ADL scores is important and clinically meaningful. However, if one inspects the means, the differences are slight, notwithstanding the statistical significance of the results. This example further illustrates the problems of interpretation that may arise from focusing on the level of statistical significance and not on the effect sizes shown by the data.

When we say that the findings are clinically or practically significant we mean that the effect is sufficiently large to influence clinical practices. It is the health workers rather than statisticians who need to set the standards for each health and illness determinant or treatment outcome. After all, even relatively small changes can be of enormous value in the prevention and treatment of illnesses. There are many statistics currently in use for determining effect size. The selection, calculation and interpretation of various measures of effect are beyond our introductory book, but interested readers can refer to Sackett et al (2000).

Effect size with discontinuous data

For a randomized controlled trial (RCT), cohort or case-control study with two groups, effect sizes correspond to the size of the difference between the two groups. For dichotomous data, measures of effect size include the odds ratio, the absolute risk reduction and the relative risk reduction.

As we discussed in Chapter 15, odds ratio (OR) compares the odds of the occurrence of an event for one group with the odds of the event for another group. For an RCT, the odds ratio compares the odds of an event for the intervention group with the odds for the control group. For example, the odds for each group, of having type 2 diabetes, in the hypothetical RCT of an exercise program for obese men, are given in Chapter 15. So, using these numbers, the odds ratio is: