Dosage calculation
Reviewing ratios and proportions
♦ A ratio is a mathematical expression of the relationship between two things.
♦ A ratio may be expressed with a fraction, such as 1/3, or with a colon, such as 1:3.
♦ A proportion is a set of two equal ratios.
♦ When ratios are expressed as fractions in a proportion, their cross products are equal.
Proportion
Cross products
2 × 10 = 4 × 5
♦ When ratios are expressed using colons in a proportion, the product of the means (middle two values) equals the product of the extremes (beginning and end values).
Proportion
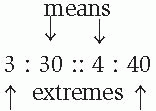
Product of means and extremes
30 × 4 = 3 × 40
♦ Whether fractions or ratios are used in a proportion, they must appear in the same order on both sides of the equal sign.
♦ When proportions are expressed as fractions, the units in the numerators (above the line) must be the same and the units in the denominators (below the line) must be the same (although they don’t have to be the same as the units in the numerators).
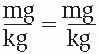
♦ If the ratios in a proportion are expressed with colons, the units of the first term on the left side of the equal sign must be the same as the units of the first term on the right side. In other words, the units of the mean on one side of the equal sign must match the units of the extreme on the other side.
mg : kg :: mg : kg
Tips for simplifying dosage calculations
Incorporate units of measure
♦ Incorporating units of measure into the dosage calculation helps prevent one of the most common errors made in dosage calculation—using the incorrect unit of measure.
♦ Keep in mind that the units of measure that appear in both the numerator and denominator cancel each other out, leaving the correct unit of measure in the answer.
♦ The following example uses units of measure in calculating a drug with a usual dose of 4 mg/kg for a 55-kg patient.
1. State the problem as a proportion.
4 mg : 1 kg :: X : 55 kg
2. Solve for X by applying the principle that the product of the means equals the product of the extremes.
1 kg × X = 4 mg × 55 kg
3. Divide and cancel out the units of measure that appear in the numerator and denominator.
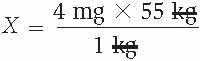
X = 220 mg
Check zeros and decimal places
♦ Suppose that you receive an order to give 0.1 mg of epinephrine subcutaneously, but the only epinephrine on hand is a 1-ml ampule that contains 1 mg of epinephrine. To calculate the volume for injection, use the ratio-andproportion method.
♦ State the problem as a proportion.
1 mg : 1 ml :: 0.1 mg : X
♦ Solve for X by applying the principle that the product of the means equals the product of the extremes.
1 ml × 0.1 mg = 1 mg × X
♦ Divide and cancel out the units of measure that appear in both the numerator and the denominator, carefully checking the decimal placement.
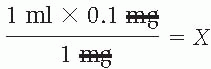
0.1 ml = X
Recheck results that seem unusual
♦ Carefully recheck any figures that seem unusual.
♦ If, for example, your calculation indicates that you should give 25 tablets, you’ve probably made an error.
♦ If you still have doubts after checking your work, review the calculations with another health care professional.
Determining the number of tablets to give
♦ Calculating the number of tablets to give lends itself to the use of ratios and proportions. To perform the calculation, follow this process:
1. Set up the first ratio with the known tablet (tab) strength.
2. Set up the second ratio with the unknown quantity.
3. Use these ratios in a proportion.
4. Solve for X, applying the principle that the product of the means equals the product of the extremes.
♦ For example, suppose that a drug order calls for 100 mg of propranolol P.O. q.i.d., but only 40-mg tablets are available. To determine the number of tablets to give, follow these steps:
1. Set up the first ratio with the known tablet (tab) strength.
40 mg : 1 tab
2. Set up the second ratio with the desired dose and the unknown number of tablets.
100 mg : X
3. Use these ratios in a proportion.
40 mg : 1 tab :: 100 mg : X
4. Solve for X by applying the principle that the product of the means equals the product of the extremes.
1 tab × 100 mg = 40 mg × X

21/2 tab = X
Determining the amount of liquid to give
♦ You can also use ratios and proportions to calculate the amount of liquid drug to give. Simply follow the same four-step process used in determining the number of tablets to give.
♦ For example, suppose that a patient is to receive 750 mg of amoxicillin oral suspension. The label reads Amoxicillin (amoxicillin trihydrate) 250 mg/5 ml and the bottle contains 100 ml. To determine how many milliliters of amoxicillin solution the patient should receive, follow these steps:
1. Set up the first ratio with the known strength of the liquid drug.
250 mg : 5 ml
2. Set up the second ratio with the desired dose and the unknown quantity.
750 mg : X
3. Use these ratios in a proportion.
250 mg : 5 ml :: 750 mg : X
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


