Although many hospitals use the unit-dose system when dispensing medicines, it is the nurse’s responsibility to determine that the medication administered is exactly as prescribed by the health care provider. To give an accurate dose, the nurse must have a working knowledge of basic mathematics. This review is offered so that individuals may determine areas in which improvement is needed. Fractions are one or more of the separate parts of a substance or less than a whole number or amount. EXAMPLE A common fraction is part of a whole number. The numerator (dividend) is the number above the line. The denominator (divisor) is the number below the line. The line that separates the numerator and the denominator tells us to divide. EXAMPLES The denominator represents the number of parts or pieces into which the whole is divided. The fraction The fraction From these two examples— EXAMPLES Decide: “Is what I need to administer to the patient a larger or smaller portion than the drug available on the shelf?” Answer: Try a second example: Decide: “Is what I need to administer to the patient a larger or smaller portion than the drug available on the shelf?” Answer: 1 Simple: Contains one numerator and one denominator: 2 Complex: May have a simple fraction in the numerator or denominator: 3 Proper: Numerator is smaller than denominator: 4 Improper: Numerator is larger than denominator: 5 Mixed number: A whole number and a fraction: 6 Decimal: Fractions written on the basis of a multiple of 10: 0.5 = When working with fractions, the rule is to reduce the fraction to the lowest terms using a common number that is found in both the numerator and denominator. Divide the numerator and the denominator by the number that will divide into both evenly (i.e., the common denominator). EXAMPLE Finding the lowest common denominator of a series of fractions is not always easy. The following are some points to remember: When denominators are the same figure, add the numerators. EXAMPLES Add the following: When the denominators are unlike, change the fractions to equivalent fractions by finding the lowest common denominator. EXAMPLE Answer Add the following: Add the fractions first, and then add the whole numbers. EXAMPLE Answer Add the following: When the denominators are unlike, change the fractions to equivalent fractions by finding the lowest common denominator. EXAMPLE Answer Subtract the following: Subtract the fractions first, and then subtract the whole numbers. EXAMPLE Answer When the denominators are unlike, change the fractions to equivalent fractions by finding the lowest common denominator. EXAMPLE Answer Subtract the following: EXAMPLE Answer 1 Place the whole number over 1 ( 2 Multiply the numerators (top numbers), and then multiply the denominators (bottom numbers). 3 Change the improper fraction to a mixed number. Multiply the following: EXAMPLE EXAMPLE Answer: Change the mixed numbers (i.e., a whole number and a fraction) to improper fractions (i.e., the numerator is larger than the denominator). 1 Multiply the denominator by the whole number, then add the numerator: 2 Multiply the numerators, and then multiply the denominators. Multiply the following: 1 Change the division sign to a multiplication sign. 2 Invert the divisor, which is the number after the division sign. 3 Reduce the fractions with the use of cancellation. EXAMPLE 1 Change the mixed number to an improper fraction. 2 Change the division sign to a multiplication sign. EXAMPLE A fraction can be changed to a decimal form by dividing the numerator by the denominator. EXAMPLE Change the following fractions to decimals: EXAMPLE EXAMPLE When fractions are written in decimal form, the denominators are not written. The word decimal means “10.” When reading decimals, the numbers to the left of the decimal point are whole numbers. It may help to think of them as whole dollars. Numbers to the right of the decimal are fractions of the whole number and may be thought of as cents. EXAMPLE Numbers to the right of the decimal point are read as follows: EXAMPLE Here is another way to view the reading of decimals: EXAMPLE (NOTE: Hospital policy now recommends that 1.000 g be written as “1 g” to avoid error. Often, the decimal point is not recognized, and very large doses have been accidentally administered. The rule is as follows: “Don’t use trailing 0s to the right of decimal points.”) EXAMPLES Note in the last example that the first number after the decimal point in the answer is 5. Instead of the answer remaining 4.5, it becomes the next whole number, which is 5. This would be true if the answer were 4.5, 4.6, 4.7, 4.8, or 4.9. In each case, the answer would become 5. If the answer were 4.1, 4.2, 4.3, or 4.4, the answer would remain 4. When the first number after the decimal point is 5 or above, the answer becomes the next whole number. When the first number after the decimal point is less than 5, the answer becomes the whole number in the answer. EXAMPLE There are two decimal places in 3.75 and one decimal place in 0.5, which means that the answer should have a total of three decimal places. Count three decimal places from the right. EXAMPLES a Multiply 223 by 0. Write the answer (0) in the unit column of the answer. b Then multiply 223 by 4. Write this answer in front of the 0 in the product. a First, multiply 124 by 4. The answer is 496. b Now multiply 124 by 0. Write the answer (0) under the 9 in 496. c Multiply 124 by 3. Write this answer in front of the 0 in the product. EXAMPLES EXAMPLES Change the following: Divide the numerator of the fraction by the denominator. EXAMPLE Change the following: 1 Divide the smaller number by the larger number. 2 Multiply the quotient by 100, and then add the percent sign. EXAMPLE A certain 1000-part solution is 10 parts drug. What percent of the solution is drug? EXAMPLES Change the following: EXAMPLES Change the following: Note that, in these examples, those numbers that were already hundredths (i.e., 10%, 15%, 25%, 50%) merely need to have the decimal point placed in front of the first number, because they are already expressed in hundredths, whereas 1%, 2%, 4%, and 5% needed to have a zero placed in front of the number to express them as hundredths. Change these percents to decimal fractions:
A Review of Arithmetic
![]() http://evolve.elsevier.com/Clayton
http://evolve.elsevier.com/Clayton
Fractions
Objective
Key Terms
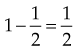
Common Fractions
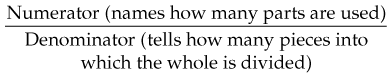
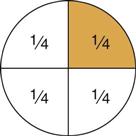
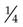 means, graphically, that the whole circle is divided into four (4) parts; one (1) of the parts is being used.
means, graphically, that the whole circle is divided into four (4) parts; one (1) of the parts is being used.
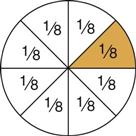
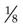 means, graphically, that the whole circle is divided into eight (8) parts; one (1) of the parts is being used.
means, graphically, that the whole circle is divided into eight (8) parts; one (1) of the parts is being used.
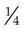 and
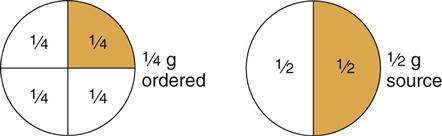
and 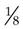 —you can see that the larger the denominator number, the smaller the portion is (i.e., each section in the
—you can see that the larger the denominator number, the smaller the portion is (i.e., each section in the 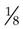 circle is smaller than each section in the
circle is smaller than each section in the 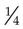 circle). This is an important concept to understand for people who will be calculating medicine doses. The medicine ordered may be
circle). This is an important concept to understand for people who will be calculating medicine doses. The medicine ordered may be 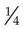 g, and the drug source available on the shelf may be
g, and the drug source available on the shelf may be 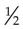 g. Before proceeding to do any formal calculations, you should first decide if the dose you need to give is smaller or larger than the drug source available on the shelf.
g. Before proceeding to do any formal calculations, you should first decide if the dose you need to give is smaller or larger than the drug source available on the shelf.
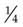 g is smaller than
g is smaller than 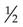 g; thus, the dose to be administered would be less than one tablet.
g; thus, the dose to be administered would be less than one tablet.
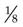 g is ordered; the drug source on the shelf is
g is ordered; the drug source on the shelf is 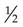 g.
g.
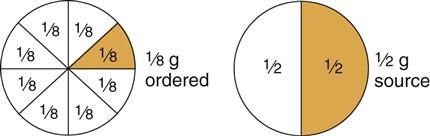
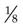 g is smaller than
g is smaller than 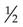 g; thus, the dose to be administered would be less than one tablet.
g; thus, the dose to be administered would be less than one tablet.
Types of Common Fractions
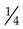 ,
, 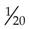 ,
, 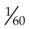 ,
, 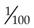
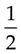 over 4 =
over 4 = 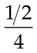
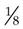 ,
, 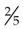 ,
, 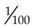
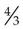 ,
, 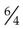 ,
, 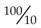
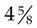 ,
, 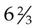 ,
, 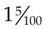
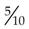 , 0.05 =
, 0.05 = 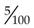 , 0.005 =
, 0.005 = 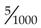
Working with Fractions
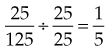
Addition
Adding Common Fractions
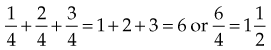
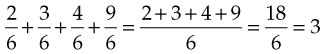
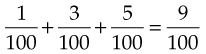
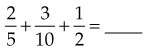
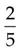 =
= 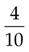
(Divide 5 into 10, and then multiply the answer [2] by 2.)
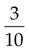 =
= 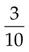
(Divide 10 into 10, and then multiply the answer [1] by 3.)
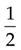 =
= 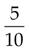
(Divide 2 into 10, and then multiply the answer [5] by 1.)
4 + 3 + 5 = 12
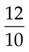 =
= 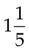
(Add the numerators, and then place the total over the denominator [10]. Convert the improper fraction to a mixed number, and then reduce it to its lowest terms.)

Adding Mixed Numbers
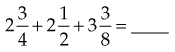
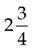 =
= 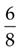
(Divide 4 into 8, and then multiply the answer [2] by 3.)
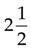 =
= 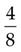
(Divide 2 into 8, and then multiply the answer [4] by 1.)
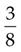 =
= 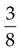
(Divide 8 into 8, and then multiply the answer [1] by 3.)
6 + 4 + 3 = 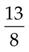
(Add the numerators, and then place the total over the denominator [8].)
2 + 2 + 3 = 7
(Add the whole numbers.)
7 + 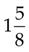 =
= 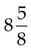
(Convert the improper fraction 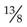 to a mixed number
to a mixed number 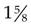 , and then add it to the whole numbers.)
, and then add it to the whole numbers.)

Subtraction
Subtracting Fractions
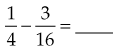
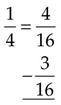
(Divide 4 into 16, and then multiply the answer [4] by 1.)
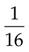
(Subtract the numerators, and then place the total [1] over the denominator [16].)

Subtracting Mixed Numbers
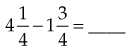
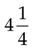 =
= 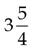
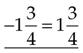
(NOTE: You cannot subtract 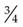 from
from 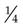 ; therefore, borrow 1 [which equals
; therefore, borrow 1 [which equals 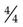 ] from the whole numbers, and then add
] from the whole numbers, and then add 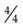 +
+ 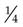 =
= 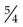 .)
.)
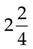 =
= 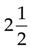
(Subtract the numerators, then place the answer over the denominator [4]. Reduce to lowest terms, and then subtract the whole numbers.)

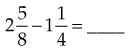
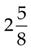 =
= 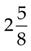
(Divide 8 into 8, and then multiply the answer [1] by 5.)
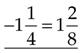
(Divide 4 into 8, and then multiply the answer [2] by 1.)
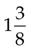
(Subtract the numerators, and then place the total [3] over the denominator [8]. Reduce to lowest terms, and then subtract the whole numbers.)

Multiplication
Multiplying a Whole Number by a Fraction
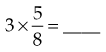
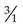 ).
).
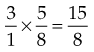
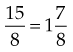
Multiplying Two Fractions
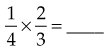
Multiplying Mixed Numbers
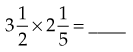
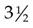 becomes 3 × 2 = 6 + 1 =
becomes 3 × 2 = 6 + 1 = 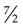
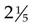 becomes 2 × 5 = 10 + 1 =
becomes 2 × 5 = 10 + 1 = 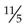
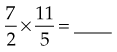
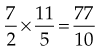
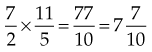
Division
Dividing Fractions
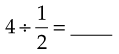
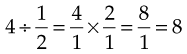
Dividing With a Mixed Number
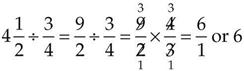
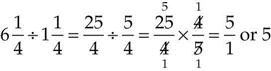
Fractions as Decimals
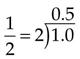
Using Cancellation to Speed Your Work
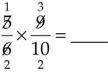
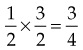
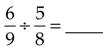
(Change the division sign to a multiplication sign, invert the divisor, reduce, and then complete the multiplication of the problem.)
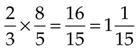

Decimal Fractions
Objectives
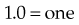
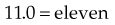
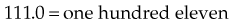
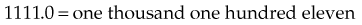
Decimals
Fractions
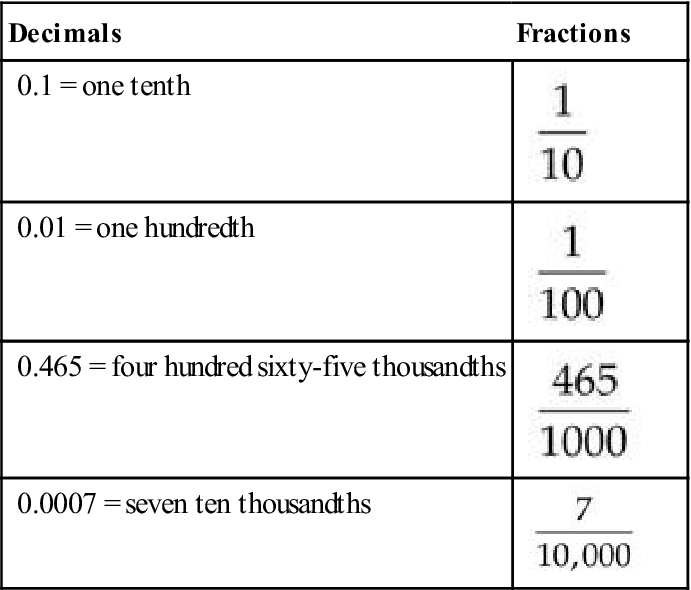
0.1 = one tenth
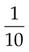
0.01 = one hundredth
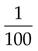
0.465 = four hundred sixty-five thousandths
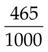
0.0007 = seven ten thousandths
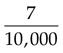

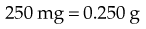
Multiplying Decimals
Multiplying Whole Numbers and Decimals
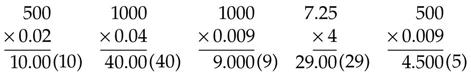
Rounding the Answer
Multiplying a Decimal by a Decimal
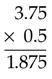
Multiplying Numbers With Zero
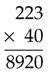
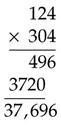
Dividing Decimals
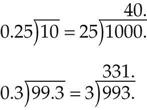
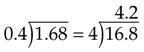
Changing Decimals to Common Fractions
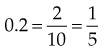
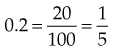
Changing Common Fractions to Decimal Fractions
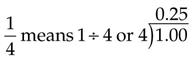
Percents
Objective
Determining the Percent That One Number Is of Another
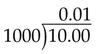
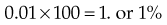
Changing Percents to Fractions
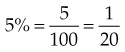
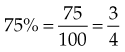
Changing Percents to Decimal Fractions
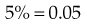
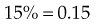
< div class='tao-gold-member'>
![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


6. A Review of Arithmetic
Only gold members can continue reading. Log In or Register to continue
 ) (
) ( ) (
) (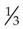 =
= 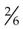
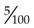 = _____
= _____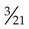 = _____
= _____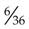 = _____
= _____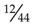 = _____
= _____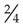 = _____
= _____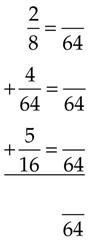
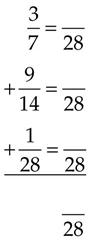
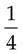 +
+ 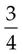 =
= 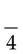
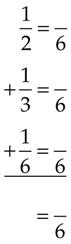
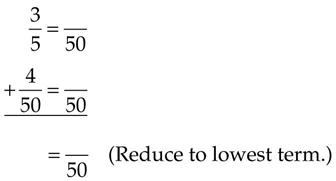
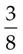 −
− 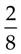 =
= 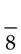
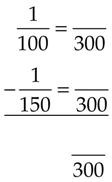
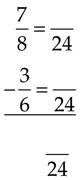
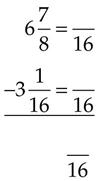
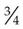 = _____
= _____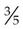 = _____
= _____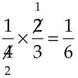
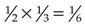
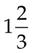 ×
× 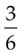 = _____
= _____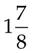 ×
× 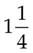 = _____
= _____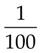 = _____
= _____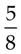 = _____
= _____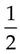 = _____
= _____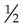 means ______
means ______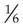 means ______
means ______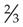 means ______
means ______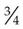 means ______
means ______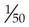 means ______
means ______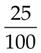 = _____
= _____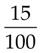 = _____
= _____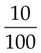 = _____
= _____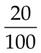 = _____
= _____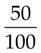 = _____
= _____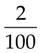 = _____
= _____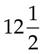 % =
% = 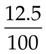 = _____
= _____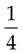 % =
% = 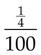 = _____
= _____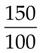 = _____
= _____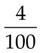 = _____
= _____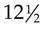 % = _____
% = _____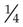 % = _____
% = _____