We can also see from Table 1.1 that, if we just happened to have a population of 200 patients with acute abdominal pain, of whom 100 had acute appendicitis and 100 did not (a prevalence of 50%) then the probability that someone with right lower quadrant pain would have acute appendicitis (the positive predictive value of the sign) is 80/(80+10) or about 89%.
However, we can see that if the prevalence of acute appendicitis in the population being assessed is much lower, say 1%, the table looks quite different. Now there are roughly 100 times as many people without acute appendicitis as with acute appendicitis (the column on the right has 10 000 patients rather than 100 patients) (see Table 1.2).
| Patients with acute appendicitis (100) | Patients without acute appendicitis (10000) | |
| Right lower quadrant pain | 80 | 1000 |
| No right lower quadrant pain | 20 | 9000 |
| Sensitivity = 80/100 | Specificity = 90/100 |
The sensitivity and specificity are the same (the reason why they are defined in such a counterintuitive way is that they are not dependent on prevalence). However, the positive predictive value of right lower quadrant pain is now only 80/(1000 + 80) or about 7%.
The positive predictive value of a clinical feature is highly dependent on the prior probability or the prevalence in the studied population. Most people with night sweats in an oncology unit will have lymphoma or opportunistic infections. Most people in general practice will not.
However, what we really want to know is how useful a clinical feature is for helping us avoid diagnostic errors. Likelihood ratios quantify the discriminatory value of a clinical feature.
The positive likelihood ratio LR+ is the probability of a positive test result in patients with the disease, divided by the probability of a positive test result in patients without the disease. This is:
LR+ = sensitivity/(1-specificity).
The negative likelihood ratio (LR−) is the probability of a negative test result in patients with the disease, divided by the probability of a negative test result in patients without the disease. This is:
LR- = (1-sensitivity)/specificity
The full Bayesian equation is that:
Post-test odds of disease = the pre-test odd of disease x the likelihood ratio
where the odds of disease is (probability of disease/(1-probability of disease).
For our purposes we would very rarely use that equation. However, lists of positive and negative likelihood ratios are useful because they give us an idea of how good a particular feature is at helping us discriminate between those with the disease and those without.
A positive likelihood ratio (LR+) of 5 to 10 is very helpful. A value of 2 to 5 is quite helpful.
A negative likelihood ration (LR-) of 0.2 to 0.1 is very helpful. A value of 0.5 to 0.2 is quite helpful.
A LR close to 1 is useless.
We can illustrate this with figures taken from the article cited above on acute appendicitis. This is reproduced in Table 1.3.
Table 1.3 The sensitivity, specificity, positive and negative likelihood ratios for certain signs and symptoms of acute appendicitis.
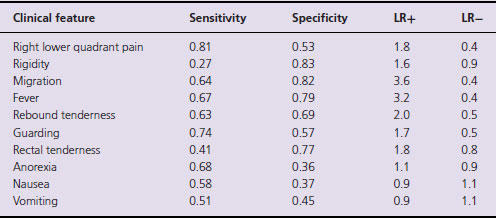
We can see that, as we would expect, the presence or absence of right lower quadrant pain is quite helpful in discriminating between those with and without acute appendicitis. Nevertheless, relying on this feature alone will miss 19% of all cases of appendicitis. On the other hand the presence or absence nausea, vomiting or anorexia is largely useless. The LRs are too close to 1.
Likelihood ratios are also useful in defining the standard required of a general practitioner. 10 or 20 years ago it was accepted clinical wisdom that a digital rectal examination (DRE) was necessary in the assessment of acute abdominal pain (‘put your finger in it or put your foot in it’). Many general practitioners were found in breach of duty for failing to carry out a DRE in a patient who subsequently was diagnosed with acute appendicitis. Studies such as those used to make the table above have shown that DRE is not generally useful in nonspecialist hands in making the diagnosis. The LR is close to 1 and it is now accepted that it should not be done in primary care as part of the assessment of someone with acute abdominal pain.
A last example of the usefulness of such tables is in the assessment of acute back pain. In the 1990s the Royal College of General Practitioners published a list of ‘Red Flags’ for people with back pain. These were clinical features that should cause general practitioners to be alerted to the possibility that the cause was not simple self limiting back pain. These features were as follows:
- Presentation under age 20 or onset over 55
- Nonmechanical pain
- Thoracic pain
- Past history – carcinoma, steroids, HIV
- Unwell, weight loss
- Widespread neurological symptoms or signs
- Structural deformity.
In cases that are brought against general practitioners for failure to diagnose or refer spinal cancer or infections the allegation is often that one or more of the first 3 ‘Red Flags’ were present and mandated investigation. In fact studies show the following ‘performance characteristics’ for 4 of the features listed (Deyo et al., 1992) (see Table 1.4).
Table 1.4 The sensitivity, specificity, positive and negative likelihood ratios for certain signs and symptoms in the assessment of acute back pain.
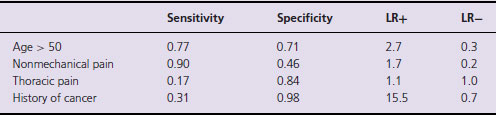
What Table 1.4 shows clearly is that the presence of thoracic back pain (versus lumbar pain) is not useful as a discriminator. It is equally likely to occur in patients with or without cancer. A past history of cancer, on the other hand, is a powerful ‘Red Flag’ for cancer. It is absent in 98% of people with simple low back pain and present in 31% of those with vertebral metastases. Since plain X-rays only have a sensitivity of 70% for detecting cancer, one can infer that a patient with back pain and a history of cancer (particularly those cancers that tend to metastasize to bone such as breast, colon, prostate, lung, renal) probably needs an isotope bone scan.
Tables 1.3 and 3.4 also illustrate the usefulness of the acronyms SpIN (when a specific test is positive, it rules the diagnosis in) and SnOUT (when a sensitive test is negative, it rules the diagnosis out). In primary care the SpINs tend to be more plentiful and useful than the SnOUTs.
If we look again at Table 1.4 we see that the specificity of the history of cancer is 98%. That is to say that most people without vertebral metastases do not have that feature. If it is present it should ring alarm bells. If a clinical feature has a high specificity (Sp) but is Positive then the general practitioner should consider the possibility of serious disease firmly ruled IN.
SnOUTs are rarer in general practice. It is instructive to look at where errors are made because the doctor has considered that a negative finding on a test rules the condition out, when in fact it does not. Examples would be cervical smear tests or plain vertebral X-rays for metastases. The smear test has a sensitivity of about 80% for cervical cancer. That means that a general practitioner should not rely on a negative smear to rule out cancer because the sensitivity is too low. 20% of cases would be missed. It is not an adequate SnOUT. The same argument is true for plain X-rays looking for vertebral metastases.
An example of a SnOUT that is often quoted, and is useful if you are good with an ophthalmoscope, is the absence of retinal vein pulsations at the disc. This sign is present in all cases of raised intracranial pressure (sensitivity is 100%) (Jacks & Miller, 2003). Thus if retinal pulsations can be seen (the sign of absent pulsations is itself absent!) it rules the condition out. Thus, in a young person with a headache, if you can see retinal pulsations at the disc (and one often can in a young person) it rules the condition of raised intracranial pressure (from a tumour or benign intracranial hypertension) out.
References and further reading
Deyo RA, Rainville J, Kent DL (1992) What can the history and physical examination tell us about low back pain? JAMA 268: 760–5.
Doust J (2009) Using probabilistic reasoning. BMJ 339: b3823.
Gill CJ, Sabin L, Schmid CH (2005) Why clinicians are natural Bayesians. BMJ 330: 1080–3.
Jacks AS, Miller NR (2003) Spontaneous retinal venous pulsation: aetiology and significance. J Neurol Neurosurg Psychiatry 74: 7–9.
Pauker SG, Kassirer J (1980) The threshold approach to clinical decision making. New England Journal of Medicine 302: 1109
Sackett DL (1992) A primer on the precision and accuracy of the clinical examination. JAMA 267: 2638–44.
Tze-Wey Loong (2003) Understanding sensitivity and specificity with the right side of the brain. BMJ 327: 716–19.
Wagner JM, McKinney WP, Carpenter JL (1996) Does this patient have appendicitis? Journal of the American Medical Association 276: 1589–93.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


