CHAPTER 23. Physics, Restraints, and Fractures
David J. Porta and William S. Smock
In many forensic cases, injury reconstruction is a critical component. Whereas engineers and specially trained police officers are skilled at reconstructing the motion of vehicles in an accident, it usually takes a person with intimate knowledge of anatomy as well as a basic understanding of physics to reconstruct how a particular occupant motion led to a specific injury. Much of the physics can be found in a general college physics course, but there are numerous reference texts worth exploring (e.g., Brach and Matthew Brach, 2005 and Rivers, 2006).
Physics
Injuries involve motion. To understand motion, it is important to begin with some principles of basic physics. The simplest measurements are scalar quantities—that is, they can be described by a single number (and appropriate units) with no mention of direction and other such factors. These include mass (M), temperature (T), time (t), and distance (D) (e.g., length, height, width, and circumference). These scalar quantities can be combined to give us a more detailed manner of describing motion. Velocity (V) and speed (S) are often used interchangeably, and it usually makes no difference in forensic cases. However, using the strict definitions in engineering or physics, velocity is a vector quantity; that is, it should have both magnitude and direction (e.g., 30 mph south). When we ignore the direction, we are simply referring to speed (e.g., 30 mph). Please note that most of the following descriptions are vector quantities. This means they should technically include a magnitude and direction. Another way of looking at this is to note that it is not just a number describing a motion, but how this motion occurs. Speed is a measure of how fast or slowly something moves. That, in and of itself, is not enough information to show that something is or is not injurious. A basketball moving at 25 mph is not injurious if it does not hit you. In fact, even if it does hit you, it might not cause an injury, depending on the angle of impact and how your body responds. When dealing with humans, it is important to include considerations of anatomy and physiology. That 25-mph basketball might be easily caught by a pair of skilled hands. But if the same ball, moving at the same speed, were to strike a single finger at the tip of the long axis of the digit, it could result in a fracture or at least a soft tissue injury.
Velocity = distance/time
Velocity equals the distance traveled over a period of time (V = D/t) in a particular direction and is often measured in miles per hour (mph), feet per second (fps), kilometers per hour (kph), or meters per second (m/s). Velocity is an important consideration in assessing injury potential as well as other factors (Box 23-1). If forced to choose between being struck by a baseball traveling at 20 mph or a baseball traveling at 100 mph, all but our masochistic readers would choose the 20 mph impact. The reason is simple; it will hurt less. At very low velocities, one would not expect serious injuries, but at higher velocities, injury severity will generally increase. At some point, injury will be maximal and even higher velocities will be irrelevant. For example, a pedestrian run over by a large truck going 50 mph will be just as dead as the pedestrian run over by the same truck at 100 mph. The only difference will likely be how far the pieces are scattered at the accident scene.
Box 23-1
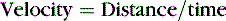
Consider that a human eye blinks in approximately 0.4 second. If one is driving on the interstate at 70 mph, how much of the roadway is missed with each blink?
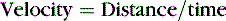
This can be rearranged to solve for D, such that D = Vt. Also, mph may be converted to feet per second (fps) by multiplying it by 1.46667, thus 70 mph is equivalent to 102.7 fps. When we solve for D, we see that 102.7 ft/s × 0.4 s = 41 ft. Therefore, with each blink of the eye, your vehicle travels 41 feet down the road. Imagine how much of the roadway is missed while adjusting the music, tending to passengers, or dialing a cell phone!
Delta V
In the study of accidents, one often hears discussion of the “change in velocity” or “delta V” (a.k.a. ΔV). Occasionally it is noted that a higher delta V indicates greater injury potential. As used in the engineering literature, this is generally true. However, one must keep in mind that the engineers and accident reconstructionists are assuming this delta V occurs over a very short period of time.
When traveling to work in a car, bus, or train, a person may zoom along at 45 mph and at some point slow to a stop for a traffic light or a stopped vehicle. If we contrast this with the force generated by someone who falls 68 feet from a sixth-story window, that person will reach a velocity of 45 mph just before striking the concrete below (Box 23-2). Both people will have changed their velocity from 45 mph to 0 mph, so they each experienced a delta V of 45 mph. In the first, virtually any member of our society would be able to bear this delta V with no problem. However, the change in velocity during the second scenario would certainly be injurious, if not fatal for most people. Obviously the difference is the amount of time it took for this change in velocity to occur. In the latter example, the change in velocity occurred over a very short period of time with disastrous consequences. Our body simply cannot maintain its structure when asked to change speed so quickly. When we look at a change in velocity over time, we call this acceleration (when the velocity is increasing) or deceleration (when the velocity is decreasing). Engineers may also refer to these as positive or negative acceleration, respectively.
Box 23-2
| Approximate Drop Height in Feet | Approximate Velocity at Impact in MPH |
|---|---|
| 10 | 17.3 |
| 15 | 21.2 |
| 20 | 24.5 |
| 25 | 27.4 |
| 30 | 30.0 |
| 40 | 34.6 |
| 50 | 38.7 |
| 60 | 42.4 |
| 70 | 45.8 |
V = square root of 2 gh, where g (gravity) = 32.2 ft/s 2 and h = drop height in ft. Note that this results in a velocity expressed as ft/s. To convert this to mph, simply multiply ft/s by 0.6818. For those more interested in metrics, g is expressed as 9.8 m/s 2 and h is drop height as measured in meters. The result would be a velocity in m/s. These calculations do not take into account resistance encountered by wind/atmosphere, but the effect is negligible at low drop heights. Note that mass is also not a concern. If one were to drop an 8-lb bowling ball from 20 feet, and a 16-lb bowling ball from 20 feet at the same time, they would both hit the ground at the same time and both would be traveling 24.5 mph. However, if one dropped an 8-lb bowling ball and a loosely wadded piece paper, the bowling ball would hit first because the paper would be affected by wind resistance. Fortunately, when examining the fall of a person from a relatively short height, resistance (a.k.a. drag) is negligible.
Terminal velocity
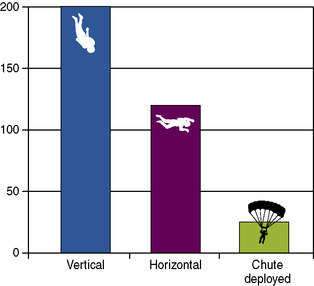
In falls from great heights, wind/atmosphere resistance (drag) plays a much greater role in determining the speed at which we strike the ground. When skydivers jump from a plane, they accelerate toward the earth. However, after a short time, they reach a point during the fall when velocity no longer changes. This is called terminal velocity. The reason is that the wind resistance encountered during the fall will not permit the skydiver to go any faster. As Figure 23-1 shows, a skydiver falling horizontal to the ground with arms and legs outstretched will achieve a terminal velocity of about 120 mph. However, if he decreases drag by angling head first toward the ground with all extremities adducted, he can increase the speed to about 200 mph before wind resistance stops the acceleration. The skydiver does not stop, of course; he stops going faster and faster and maintains a constant velocity until reaching the ground—assuming that the parachute is not opened. Deployment of a parachute greatly increases the drag and the terminal velocity will fall to a level that is far more tolerable to the body.
Acceleration/deceleration
Injuries may occur when a body, or body part, is accelerated or decelerated more rapidly than our tissues can accommodate. For instance, if a hand is slowly rubbed across someone’s face in the area of the mouth, the skin might be stretched a bit, but the elastic nature of the skin and hypodermis will accommodate this action with no untoward consequences. However, if there were a more rapid acceleration of this same skin (i.e., a violent slap), greater potential for injury would exist. A small blood vessel might have been stretched too quickly, resulting in a rupture, and blood would leak into the surrounding tissues creating a hematoma or bruise. Inside the mouth, there might be a tear of the labial frenulum.
Acceleration and deceleration injuries both relate to inertia. Sir Isaac Newton (1643–1727) taught us that a body in motion wants to stay in motion until acted on by an external force. The opposite is also true; a body at rest will tend to stay at rest until acted on by an external force. The human body is fairly well equipped to deal with changes in inertia. In fact, some publications have even attempted to document a human’s ability to cope with everyday accelerations (Allen et al., 1994, Funk et al., 2007 and Ng et al., 2006).
Although it is difficult to assess the relative incidence of acceleration versus deceleration injuries, it is not difficult to illustrate examples of each. Acceleration injuries include the following: (1) A person is stopped in her car when her vehicle is violently impacted by a truck. Her body might accelerate faster than her head and neck, and this might result in a cervical or head injury. (2) A pedestrian crossing the street is struck on the leg by a passing car. The impacted portion of the tibia is accelerated faster than the bone can handle and a fracture results. (3) A boxer punches his opponent’s head. This accelerates the cranium more quickly than the cervical vertebrae. The result is a pinching of the brain stem near the foramen magnum, which temporarily affects the reticular formation and causes the loss of consciousness. (4) Lastly, a gunshot wound is a horrible example of an acceleration injury. If we took a bullet and tossed it at a person’s abdomen, it would bounce off harmlessly. The skin would tolerate the impact of a low mass bullet traveling at very low speed. The abdominal skin in the area of impact, with no initial velocity, would be able to deform or dimple as it accelerated while absorbing the energy of impact. However, the same low mass bullet, when fired from a gun, now has tremendous velocity. As the fired bullet contacts the skin, the skin cannot accelerate quickly enough to accommodate the force and it tears along with the deeper tissues that are penetrated.
Examples of deceleration injuries are also easily conjured. Falls have been mentioned previously, but it would be wise to remember the cliché “It’s not the fall that kills you—it’s the sudden stop!” Sporting accidents are probably responsible for producing the greatest number of deceleration injuries—for example, a skier striking a tree, a volleyball player rolling an ankle while landing on another player’s foot, or a tackler compressing his spine while spearing an opponent. Athletes certainly experience a large number of deceleration injuries, but the really serious ones are rare. Motor vehicle accidents likely give rise to the greatest number of serious deceleration injuries (head-on collision, rollover, ejection, underride, etc.).
Force = mass × acceleration
Often when a person is injured, one of the questions for a forensic investigator is “How much force was involved?” It seems attorneys and perhaps juries would like a simple number on which to make judgments. Such simplifications should be avoided. A thorough understanding of force is necessary before attempting to use it in the description of a mechanism of injury. Quantifying a force is often not nearly as important as describing how the force was applied. Remember, force is a vector, not a scalar quantity. Force involves mass. It was previously noted that mass typically has no significant effect on the velocity of a human body falling from short heights. However, when the victim strikes the ground with an abrupt deceleration, mass does come into play. The cliché “The bigger they are, the harder they fall” is completely true. Why can an insect fall the equivalent of 20 times its body height with no apparent injury, but a person falling 20 times his or her height will almost surely die? The difference is related to the mass (weight). Falling occurs at a constant acceleration (gravity). Force is the result of mass × acceleration, so a creature or object with more mass will strike the earth with more force and thus there is more potential for injury.
It is obvious that a falling mass will cause more damage if it falls or is dropped from a higher distance. Occasionally, one hears of the supposed fact that if a 200-lb person falls or jumps from a certain height, the effective weight is doubled or tripled. As with most popular misuses of physics, there is a hint of truth behind this, but critical details never seem to be included. It is true that the potential energy varies with both mass and drop height. Potential energy is defined as mass × gravity × height of the drop and yields energy values (e.g., foot-pounds in U.S. units, or Joules in metric units, not pounds force). The impacting force is highly dependent on the give of the impacter and/or impacted surface. If a 200-lb man stands on someone’s foot, he exerts 200 lbs of force on it. If he jumps off a 6-inch curb landing with both feet on the same foot, it will be perceived by the victim to be much more than 200 lbs. The give is the important detail that is often missing when one is asked “how much more force does a 200-lb man exert when he jumps 6 inches onto a surface?” There is a simple formula for figuring this out, but there are important assumptions that need to be clearly stated: (1) To maximize the effect, the man must keep his joints very rigid (i.e., no bending at the knee, hip, or spine)! (2) The amount of give is the deformation of the foot from soft tissue compression and the like, plus the give in the soft tissues or shoes worn by the jumper. It would be estimated to be about 2 inches in this case illustration. Therefore, if a 200-lb man rigidly jumps 6 inches onto another person’s foot, it would result in about 1200 in pounds of force. However, this must be divided by the give, so 1200/2 = 600 lbs of force. Thus, under these conditions/assumptions, the man’s impacting force tripled his weight when he jumped 6 inches. It is very important to note that had the man flexed his ankle, his knee, his hip, and his spine, the effective force would have been much lower. Consider the high-flying maneuvers in the wrestling entertainment arena (Fig. 23-2). A 200-lb man may jump off the ropes and fly 100 inches down to land on his opponent. His impact force is never 10,000 lbs [(200 lb × 100 inches) / 2 inches]. There are several reasons why there is no major injury: (1) He does not land with all his weight on one relatively small area (e.g., his feet planted on his opponent’s head); (2) he maximizes the amount of give in his body by flexing at multiple joints; (3) his opponent also maximizes his give by flexing several joints and collapsing his body at impact; and (4) the wrestling mat is designed to provide several inches of give as well. But even understanding force from falls is insufficient when studying a mechanism of injury.
Stress = force per unit area
As noted earlier, it is a common mistake to make generalizations about a supposedly injurious force without defining how it is applied. Recall that force is mass × acceleration. Once again, using a dropped object as an example, it is easy to understand the importance of how a force is applied. If a 2-lb knife is dropped 4 feet from one’s hand, it will have a certain force. If it lands horizontally on a foot, it will bounce off harmlessly. If it lands on the point of the blade, it will quite likely penetrate the foot and cause an injury. The force in these two examples is the same (same knife mass, same drop height, same gravity, and same amount of give in the foot). The difference here is in the area on which the falling force was allowed to act. If force is applied to a small area, it has much greater injury potential than if it is were applied over a larger area. This is the engineering concept of stress. Stress is force per unit area (e.g., pounds per square inch or psi in U.S. units, Paschals in metric).
Design engineers know all too well the value of these factors. A relatively tiny amount of padding can make huge differences in the injury potential of a dashboard, shin guard, or helmet. Even better than padding is the control of deceleration. If one lengthens the time of deceleration, a great number of injuries may be mitigated. This is the basis for the development of seat belts, air bags, collapsible steering columns, laminated glass, energy-absorbing bumpers, crumple zones, and other features (Holt, 2005). All of these are designed to allow a moving person to slow down over a longer period of time (sometimes referred to as ride down time in motor vehicle collisions). A relatively tiny increase in ride down can mean the difference between life and death.
Engineering design challenges
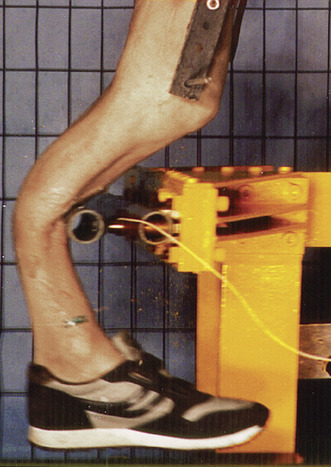
If one merely wanted to stop an object, it is relatively easy to accomplish this through design. For example, let us imagine that a vandal has been throwing eggs and breaking a window of a residence. If the homeowner wanted to design a window that would be break resistant, a few assumptions would be needed about the dimensions and mass of a typical egg as well as the speed at which it could be thrown. To simply stop the egg, a break-resistant window could be installed that would resist the stress of the thrown egg. However, even with this new window in place, the homeowner would still be required to clean up the mess from the shattered eggs on the window. To get an idea of the challenges that design engineers face, assume the egg is your head and it is hurled at the windshield of the car you are driving as you crash into another vehicle. It would be easy to design a windshield that keeps your head in the car, but the trick is to also keep your head from shattering. This is why biomechanics researchers will often subject cadavers or cadaver parts to impact studies (Fig. 23-3). The idea is to develop an understanding of how bodies or body parts move when subjected to injurious forces and try to establish tolerance curves. This data may ultimately be used to design crash test dummies or computer modeling programs, which, it is hoped, will translate into producing safer vehicles, sporting gear, and work environments.
It should be noted that design engineers in virtually all arenas continually attempt to improve safety, and a major way to accomplish this is to try to control acceleration/deceleration, force, and/or stress in predictable situations. For example, shin guards are designed to keep the force of an impact from being transmitted to a small portion of the leg. A small amount of padding, covered by a relatively impact-resistant shell, works very well. This spreading of the load is a key method of engineering safety. Spreading the load effectively decreases stress.
In an automotive environment, the challenge to incorporate occupant protection is quite a bit greater than designing to protect a shin from being injured by a kick in a soccer game. Crash injuries may occur because of factors such as acceleration, deceleration, rotation, intrusion, crush, and rollover, and these may occur individually, in multiples, and repeatedly.
Restraints
Seat belts
Seat belts are still the primary safety feature of motor vehicles. Although initially their design was rather simple (but still fairly effective), seat belts have evolved with advances in technology and understanding of crash forces. Modern seat belts incorporate high-tech retractors with pyrotechnic pretensioners and the latest webbing materials. The combination of spool out and belt stretch allows for a more controlled ride down of a crash. The seat belt also keeps occupants in position to take advantage of other safety designs within the vehicle (padding, air bags, etc). The only area where seat belt technology has not sufficiently improved is in the area of marketing. Seat belt use is still only approximately 83% in this country according to data available on the website of the National Highway Traffic Safety Administration (NHTSA). Seat belts may cause injuries (abrasions, lacerations, and even fractures), but safety experts agree that in the overwhelming majority of cases, the restrained occupant is trading catastrophic injuries for relatively minor ones. Here are the most common arguments made to this author by consumers not wanting to use their seat belts: (1) “I’m afraid I won’t be able to get out of the seat belt if the crash involves a fire or water submersion.” (2) “I know a guy who was in a wreck, and he wouldn’t have survived if he’d been wearing his seat belt because he was ejected from a massively crumpled car.” (3) “I rarely drive very far or on the expressway and I’m a great driver so I won’t be in an accident.” (4) “It’s uncomfortable and restricts my movement within my car.” There is insufficient space in this chapter to list all the facts from voluminous research to counter these arguments, but briefly here are some:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


Get Clinical Tree app for offline access